MTH6102: Bayesian Statistical Methods 2021
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MTH6102: Bayesian Statistical Methods
Question 1 [25 marks].
Suppose that we have data y = (y1 , . . . ,yn). Each data-point yi is assumed to be generated by a distribution with the following probability density function:
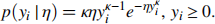
The unknown parameter is n, with 9 assumed to be known, and n, 9 3 0.
|
(a) Write down the likelihood for n given y. Find an expression for the maximum
likelihood estimate (MLE) (b) A Gamma(α,8) distribution is chosen as the prior distribution for n. Show that the posterior distribution is also a gamma distribution with parameters that you should determine. (c) We would like to choose the gamma prior distribution parameters such that the prior mean is (B + 10)/100, where B is the second-to-last digit of your ID number, and the prior coe优cient of variation (standard deviation divided by the mean) is 0.5. Find the values of α and 8 that are needed. (d) The data are y = (2, 7, 5, 3,C + 1), where C is the last digit of your ID number, with n = 5. Set 9 = 2.
(i) What is the MLE |
(ii) Using the prior distribution from part (c), what are the parameters of the posterior
distribution for n?
(iii) What are the posterior mean and standard deviation for n?
Question 2 [16 marks].
Suppose that the data y = (y1 , . . . ,yn) are a sample from a normal distribution with unknown mean θ and known standard deviation r = 2. Our prior distribution p(θ) is normal with mean 0 and standard deviation r0 .
|
(a) For an uninformative prior, do we need a large or small value for r0 ? (b) We want the prior probability P(|θ| s A + 10) to be 0.95, where A is the third-to-last digit of your ID number. What value for r0 should we choose? (c) A colleague prefers a Cauchy distribution as a prior. What is a possible reason for this preference?
Let the sample mean (d) What is the posterior distribution for θ, p(θ | y)? Based on this posterior distribution, find a point estimate for θ . |
(e) Suppose that we want to find the posterior probability P(θ s 0 | y). Write an expression for this probability in terms of ←, the cumulative distribution function for the standard normal distribution.
Question 3 [20 marks].
The data are y = (y1 , . . . ,yn), a sample from a negative binomial distribution with parameters q and r, where r is assumed to be known. A Beta(α,8) prior distribution is assigned to q. Apart from part (c), the answers do not need any numerical calculations.
In the following R code, the data y is denoted by y in the code, r is the known parameter, and alpha and beta are the prior parameters. The posterior distribution for q is Beta(a, b).
r = 2
alpha = 4
beta = 4
a = r*length(y) + alpha
b = sum(y) + beta
qbeta(0.5, shape1=a, shape2=b)
qbeta(c(0.025, 0.975), shape1=a, shape2=b)
|
(a) In statistical terms, what will the second-to-last line of code output? (b) In statistical terms, what will the last line of code output?
(c) Let B and C be the second-to-last and last digits of your ID number, respectively. Take the sample size n = B + 10, and
|
2022-01-05