Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

1.   (a) Let

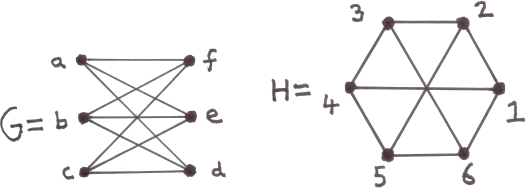
Determine if G and H are isomorphic. If G and H are isomorphic supply an isomorphism φ : V (G) −→ V (H). If not, justify your answer.         [10 Marks]

(b) Draw two non-isomorphic graphs which have degree sequence (2, 2, 2, 2, 2, 2, 2). Justify your answer.                                                                          [10 Marks]

(c) Is (4, 3, 3, 1, 1, 1, 1) the degree sequence of a tree? Justify your answer. [5 Marks]

2.   (a) Use the Erd˝os-Gallai Theorem to determine if (5, 5, 5, 4, 4, 3, 2) is a graphic sequence.                                                                                            [10 Marks]

(b) Use  the  Havel-Hakimi  algorithm  to  determine  if  (8, 7, 5, 4, 4, 3, 2, 1, 1)  is  a graphic sequence.                                                                               [10 Marks]

(c) A graph  G has degree sequence  (3, 2, 2, 2, 1, 1, 1).   Is  G isomorphic to the complete graph K7 ?                                                                            [5 Marks]

3.   (a) Explain why the hypercube graph, Qn , is bipartite and write down the partite sets for Q2  and Q3 .                                                                            [15 Marks]

(b)  Suppose that G is a 2-colourable graph with vertices coloured red and blue. Suppose that G has a Hamilton Cycle. Prove that there are the same number of red and blue vertices.                                                                    [10 Marks]

4.   (a) Let G be the graph

Find its chromatic polynomial PG (k). Hence or otherwise find G’s chromatic number.                                                                                              [15 Marks]

(b) Let K3,3  have partite sets {1, 3, 5} and {2, 4, 6}. Let G = K3,3 − {1, 4}. Show, by drawing the graph, that G is planar.                                           [10 Marks]