MATH2301, SEMESTER 2, 2021 FINAL EXAMINATION
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
![]()
![]()
![]()
FINAL EXAMINATION
MATH2301, SEMESTER 2, 2021
3. QUESTIONS
3.1. Question (10 points total). Clearly write either “True” or “False” (not both!) for each of the statements below. No justification necessary.
(1) The relation {(a, b) e N x N | b - a = 1)is a partial order relation.
(2) The language consisting of all strings such that no two 1s in the string appear in consecutive positions is a regular language.
(3) There can be two different regular expressions r1 and r2 such that L(r1 ) = L(r2 ).
(4) If a game has Grundy label 6, then it is equivalent to a nim game whose state is 4, 3, 1.
(5) In an impartial combinatorial game G, it may be possible to move directly from a P position to another P position.
|
3.2. Question (15 points total). Answer the following short questions. No justifications are required. |
|
|
(1) If p |
|
|
of the shortest path from p to q? |
|
|
(2) In the divisor poset of 48, what is the value of μ([8, 48])? |
|
|
(3) Consider the subset poset of {a, b). Letf be the element of the incidence algebra of this poset defined |
|
|
as f ([S, T ]) = |T \S|, namely the number of elements in T that are not in S. Is f invertible? |
|
|
(4) Let L1 = {010, 000)and L2 = {1, ε). List all elements of L1 o L2 . |
|
|
(5) How many winning moves are there in the nim game with position (1, 2, 3, 7)? List them all. |
|
|
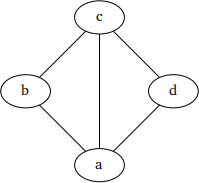
3.3. Question (10 points total). Consider the graph shown below. |
|
|
|
|
|
|
 |
|
|
|
|
(1) (4 points) What is the minimum number m of colours required for a proper m-colouring of this graph? |
|
|
Justify why you need at least m colours, and exhibit a proper m-colouring. |
|
|
(2) (6 points) Let G be this graph and let pG (k) be the number of proper k-colourings of this graph. Find |
|
|
a general formula for pG (k) by any method of your choice, justifying your work. (You may use the |
|
|
following notation if you wish: if e is an edge in G, then G\e is the graph with the edge e deleted, |
|
|
and G/e is the graph with the edge e contracted.) |
|
3.4. Question (10 points total). Consider the graph shown below.
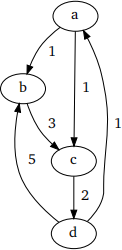
(1) (3 points) Draw the transitive closure of this graph, ignoring the weights. Justification not required.
(2) (7 points) Write down the weighted adjacency matrix using the weights shown in the diagram. Paths of length zero are considered to have weight zero. Calculate the matrix that shows the minimum weight paths between any pair of vertices. Show your work.
3.5. Question (10 points total). Consider the two posets P = {a, b, c) and Q = {x , y, z), whose Hasse diagrams are shown below.

(1) (3 points) Recall that the order relation on the product poset P x Q is that (a, β) 5 (a/ , β / ) if both a 5P a/ and β 5Q β / are true. Draw the Hasse diagram of the product of the two posets shown above, and label it clearly.
(2) (4 points) Find an interval in the product poset on which the Möbius function μ evaluates to zero. Justify briefly.
(3) (3 points) How many intervals (if any) are there in the product poset on which the Möbius function μ evaluates to zero? No justification necessary.
3.6. Question (10 points total). Consider the language L = {0, 1)on the alphabet □ = {0, 1).
(1) (3 points) Write down a 3-state NFA that recognises L . Justification is not required.
(2) (7 points) Convert your NFA to a DFA using the power set construction discussed in class. Show your work briefly.
3.7. Question (10 points total). Let □ = {0, 1). Suppose that r is some regular expression and L(r) is the language recognised by r . Let L/ be the language
L/ = {(x1y1 x2y2 . . . xk yk ) | for some k 2 0, such that each xi e □* , yj e L(r)).
(1) (4 points) Write down a regular expression that recognises L/ , in terms of r. That is, your answer is allowed to contain r . Justify your answer.
(2) (6 points) Suppose that M is a DFA or NFA such that L(M ) = L(r). For simplicity, assume that M has a single accepting state, and that the schematic of M looks like this.
![]()
![]()
![]()
![]()

Draw diagrams to show how to convert the regular expression you found in the previous problem to a DFA or NFA that recognises L/ . Alternatively, you can directly draw a DFA or NFA that recognises L/ . Justify your answer fully. Again, your answer is allowed to contain the schematic shown above.
3.8. Question (10 points total). Let □ = {0, 1). Let L be the language consisting of all strings that have length at least two, and a 1 in the second spot from the right hand end. That is,
L = {w | w = a 1b for some a e □* and b e □).
(1) (4 points) Draw a DFA or an NFA that recognises L . No justification is required.
(2) (6 points) Convert your DFA or NFA into a regular expression. Show your work in every step.
3.9. Question (15 points total). Consider the game of kayles, which is played as follows. There is a row of bowling pins, such as the following.
(● ● ● ● ●)
A move consists of knocking out either a single pin, or two consecutive pins (without any gaps in between). For example, from the configuration above, the following are two of the possible valid moves.
(● o ● ● ●) or (● &n
2021-12-26