CPT 107 Discrete Mathematics and Statistics
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
CPT 107
Discrete Mathematics and Statistics
Question 1: Proof Techniques [11 marks]
(a) Use proof by contradiction to show the following statement: if a and b are rational numbers and 
is irrational.
(5 marks)
(b)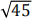 
is irrational. If you think that it is true, prove it. If not, explain why.
(4 marks)
(c) For all natural numbers m ≥ 1, use proof by induction to show that:
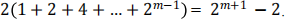
(2 marks)
Question 2: Set Theory [10 marks]
(a) Let A, B and C be non-empty sets, prove or disprove that A – C = (A – B) ∪ (C – B).
(2 marks)
(b) Let A, B and C be non-empty sets. If A ⊂ C and 
A ⊆ B ⊆ C , then either A ⊂ B or B ⊂ C . If you think that it is true, prove it. If not, explain why.
(5 marks)
(c) Prove or disprove that the empty set is a subset of every set.
(3 marks)
Question 3: Relations [21 marks]
(a) Let X = 
1,2,3
. What is the transitive closure of the relation
1, 1
, 
1,2
, 
1,3
, 
3, 1
, (2,3)
on X?
(3 marks)
(b) Let 
and S be transitive relations on a non-empty set A. Prove or disprove the following:
1. if 
2 ⊆ 
then 
is transitive.
2. ifS ∘ R ⊆ R ∘ S then R ∘ S is transitive.
(6 marks)
(c) Let X= {a, b, c, d, e} and let S be a relation on X such that:
S = {(a,a), (b,b), (c,c), (d,d), (e,e), (a,b), (a,c), (a,d), (a,e), (d,e)}. Prove or disprove that S is a partial order. If S is a partial order, draw its Hasse diagram. draw the corresponding Hasse diagram.
(4 marks)
(d) Let R and S be equivalence relations on a set Q, and T = R-1 ∩ S-1. Prove or disprove that T is an equivalence relation.
(8 marks)
Question 4: Functions [15 marks]
(a) Let 
: ℕ → ℕ and y∈ ℕ, check whether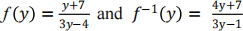 
are inverses.
(2 marks)
(b) For any non-empty set Y, there is no bijective function from Y to P(Y). If you think that it is true, prove it. If not, explain why.
(6 marks)
(c) Letf be a function from 
: ℤ → ℤ . Show the following statements are equivalent:
1. fis injective,
2. fis surjective,
3. fis bijective.
(7 marks)
Question 5: Logic [24 marks]
(a) Show whether the statements below are tautologies and/or contradictions:
1. (p ∧ 
) → (
∨ 
)
2. (
∧ 
∧ 
¬
∨ ¬
) ∧ ((p ∧ 
) → (
∨ 
))
3. 
∧ 
→ (
→ 
)
(6 marks)
(b) For each of the two cases 1. and 2. below, show whether the statement on the left-hand side is equivalent to the statement on the right-hand side:
1. (
∧ 
) ∨ (¬
∧ ¬
) ≡ 
⇔ 
2. ¬(
→ 
∧ 
→ 
) ≡ 
⇔ ¬
(6 marks)
(c) Consider the signature S = {Roommate, Male, tim, maria} consisting of a binary predicate symbol Roommate, a unary predicate symbol Male, and two constant symbols tim and maria. Assume that these symbols have the following meaning:
Roomate means “is a roommate of” (i.e., Roommate (x, y) states x is a roommate ofy).
Male means “is male” (i.e., Male(x) states x is male).
tim and maria refer to “Tim” and “Maria”, respectively.
Translate the following sentences into S-formulae, that is, for each of the following sentences provide an S-formula that expresses the sentences:
1. Maria is a roommate ofTim.
2. Tim has a male roommate.
3. All roommates ofTim are also roommates ofMaria.
4. Tim has at least 2 roommates.
5. Everybody has a roommate.
6. Nobody is a roommate of everybody else.
(12 marks)
Question 6: Combinatorics and Probability [19 marks]
(a) Jim and May have 14 children. Prove that at least two members of this family were born in the same month.
(2 marks)
(b) Consider an alphabet which consists of 26 distinct upper case letters (i.e., A …Z) and 10 distinct digits (i.e., 0 …9). Find the number of possible 6 character passwords under the following conditions:
1. Upper case letters and digits must be alternate and distinct.
2. All characters are distinct letters and must be in alphabetical order. (e.g., “ABCFGH” is allowed, but “BACDEF” is not allowed).
3. The password can only contain the upper case letters X and Y (and no digits).
4. The password can only contain the upper case letters R and S (and no digits), and must contain an equal number of each.
(8 marks)
(c) Students Tim and Pan meet in the final match of the
2021 XJTLU Pool Competition, where two students play against each other until one student wins 4 frames. Assume that:
the probability that Tim wins a frame is 0.35;
the probability that Pan wins a frame is 0.65; and
these probabilities do not change during the final match.
1. Determine that the probability that Pan wins the match without losing any frames.
2. Determine that the probability that the match ends in 5 frames.
3. Determine that the probability that Tim wins the match and the match ends in 7 frames. (6 marks)
(d) For a lottery, Tom pays $5 and then picks up a three-digit number (a digit refers to any of the numerals from 0 to 9). If the three numbers are picked in the specific order “777”, then Tom wins $1000. Calculate the expected value of his payoff.
(3 marks)
2021-12-25