ECON6032 Problem Set 2
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
ECON6032
Problem Set 2
Consider an economy populated by a representative household that lives forever. Time is discrete. Household’s preferences are given by
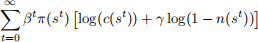
where π(sn ) is the probability of a history of stochastic and exogenous events sn = {s1 , s2 , ..., sn } given s0 , and all other variables have the usual interpretation. The budget constraint is
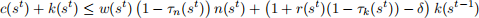
where variables have the usual meaning. Agents have rational expectations.
In each period t static firms produce final goods with a neoclassical production function of labour and capital 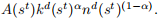
Firms sell final goods and hire labour and capital from the household in perfectly competitive markets. Feasibility requires that
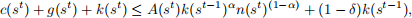
where g(sn ) > 0 is government spending, which is exogenous.
1. [15 points] Define a sequential competitive equilibrium for this economy given s0 and an initial capital stock k(s0 ).
2. [15 points] Assume that the stochastic process has a first order Markov structure so that π(sn /sn- 1 ) = π(sn /sn- 1 ). Define a recursive competitive equilibrium.
3. [30 points] First state wether the equilibria above are Pareto efficient or not. Then demonstrate your answer.
4. [10 points] Assume now that g(sn ) = 0. What is the optimal fiscal policy in this case?
5. [10 points] Studying Ramsey taxation it has been shown that the optimal policy is characterized by what amount of capital taxes in the steady state?
6. [20 points] Explain whether and how a new government would want to deviate from the Ramsey policy above.
The next are bonus questions worth 10 points each in case you have lost points in the previous questions.
7. To illustrate the trade-off between taxing capital and labour, assume that the model is deter- ministic (sn is constant over time). Assume the following parameterization: A = 1, β = 0.96, γ = 1, α = 0.36, δ = 0.1, g = 0.2. Using Matlab, or any other program of your choice, solve the model for the steady state given the following 7 values of the tax rate on capital τd = 0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.30. Note: you will have to find the corresponding τ亿 that en- sures that the government runs a balanced budget. Report, the values of consumption, labour, capital, τ亿 , and the net wage for each level of τd . The best way to report these results is through figures that plot each variable as a function of τd (the command in matlab is plot). Alternatively, you could report them in a table.
8. Use your results from the previous question to provide some intuition on your answer to question 5.
2021-12-23