闪电代写 -代写CS作业_CS代写_Finance代写_Economic代写_Statistics代写_代码代做_IT代写_加急帮助

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MATH 2100 Fall 2021

Discrete Mathematics Final Exam

1. Three elves were toiling in Santa’s workshop. When Santa comes to check on them, each makes a statement. Every elf either always lies or always tells the truth. Elf A says “Elf B and I did our work.” Elf B says “All three of us did our work.” Elf C says “Only one of us did our work.” A good elf always tells the truth and always does their work. A bad elf always lies and does not do their work. Who, if anyone, did their work? Justify your answer.

2. Prove that for any integer k, if 3k + 1 is even, then k is odd. (Hint: Use the contrapos-

itive.)

3. Prove by induction that b2 - 1 is divisible by 8 for every odd natural number b. Be sure to include the base case and induction hypothesis in your proof.

(a) Consider the set V = {a, b, c, d, e}. Deﬁne any set W such that there exists an surjective

(onto) function but not a bijection with domain W and codomain V . Write such a function f : W → V . (f must be an surjection but not a bijection.)

(b) Suppose h : X → Y is an injective (one-to-one) function and g ·h : X → Z is a bijection.

What is the domain and codomain of g. Is g necessarily an injection, surjection, or bijection? Justify your answer.

5. Write an equivalence relation on the set of natural numbers N where 2 and 9 are in the same equivalence class, 3 and 5 are in the same equivalence class, and 2 and 3 are not in the same equivalence class. Prove that your relation is an equivalence relation. If it is not possible to create such an equivalence relation, explain why not. (Hint: Equivalence classes can be ﬁnite.)

6. Which of the following sets have the same cardinality as N = {1, 2, 3, 4, 5, . . . }? Justify your answer for each set A, B, and C .

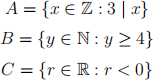
7. Alexi drew a graph with k vertices and an 2k edges. Is it possible for all the vertices of such a graph to have the same degree? If so, what is the degree of the vertices? Justify your answer.

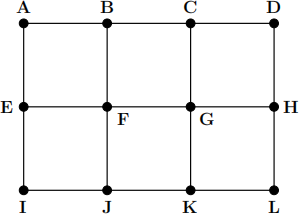
8. Eulerize the graph shown below. (Be careful that you add the minimum number of edges possible and that you add only “legal” edges.) Then use Fleury’s algorithm to ﬁnd an Euler circuit in the Eulerized graph that starts and ends at A.

9. Fernando is going to travel to Amsterdam, Budapest, Copenhagen, Lisbon, Madrid, Prague, Rome, Soﬁa, and Vienna. He wants to start in Madrid, visit each city exactly once, and cover the least amount of distance. The distances between each city are given in the table.

● If Fernando wants to guarantee that he ﬁnds the shortest such circuit, how many circuits would he have to calculate the distance for? Explain. (Please do not attempt to write out a list of the circuits that he would need to calculate the distance for.)

● Find the circuit that the“cheapest link” (also called “edge-greedy”) algorithm generates for Fernando’s problem.

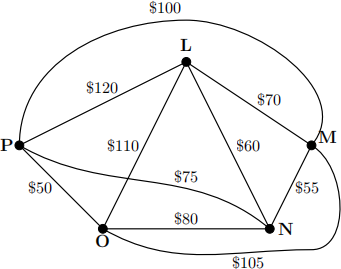
10. The weighted graph below shows the cost of traveling between ﬁve locations: L, M, N, O, and P. The goal is to ﬁnd a cheap circuit (closed path) starting and ending at M that visits L, N, O, and P exactly once each. What circuit does the “repetitive nearest neighbor” (also called “repeated vertex-greedy”) algorithm generate for this problem? How much does it cost? Show all of your work.