MATH 366: Geometry
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH 366: Geometry
![]()
![]()
1. [5] Suppose a circle ( with centre O is given. Let P be a point on (. Show how to construct the line tangent to ( at P with straightedge and compass, and prove your construction works.

2. [4] Prove that a triangle ABC is isosceles if and only if it has two equal angles.
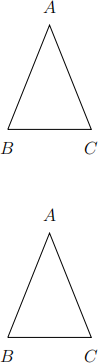
3. (a) [2] State Thales’ Theorem.
(b) [4] Prove that corresponding sides of similar triangles are proportional.
4. [3] Given a line segment of length 1, show how to construct a line segment of length C5.
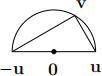
5. [4] Give a vector proof that an angle in a semicircle is a right angle.
6. [3] Explain how to construct a right triangle with given hypotenuse AB using straight- edge and compass, and why your construction works.
7. [4] Explain how to construct a square equal in area to a given rectangle using straight- edge and compass, and prove your construction works.
8. In this question the fact that two lines 11 and 12 have a common point if and only if the slope of 11 is not equal to the slope of 12 can be assumed to be known. Either slope may be infinite.
(a) [3] Let 1 be a line and P be a point not on 1. Show that there is a unique line on
P which is parallel to 1.
(b) [2] If 1 has equation y = 2x + 3, what is the equation of the parallel to 1 through
(1, 1)?
9. [3] Let A = (0, 1), B = (0, 0) and C = (1, 0). Suppose f : R2 → R2 is an isometry such that f (A) = (3, 1), f (B) = (3, 0), and f (C) = (2, 0). Let D = (2, 4). Find f (D).
10. Let A = (0, 1), B = (0, 0) and C = (1, 0). Suppose f : R2 → R2 is an isometry. In each of the following situations, determine whether f is a translation, rotation or glide reflection, and briefly explain your reasoning. Note: here, a reflection that is not
followed by a translation is regarded as a glide reflection.
(a) [2] f(A) = (_1, 2), f(B) = (_2, 2), f(C) = (_2, 1).
(b) [2] f(A) = (_0.5, 3.3), f(B) = (_0.5, 2.3), f(C) = (0.5, 2.3).
(c) [2] f(A) = (3, 2), f(B) = (3, 1), f(C) = (2, 1).
11. (a) [2] Define the cross ratio of a 4-tuple (p, q, r, s) of points on a line.
(b) [3] Suppose p = 0, q = 1 and r = 4. What value of s gives ![]() as the cross-ratio of
as the cross-ratio of
(p, q, r, s)?
12. [4] Let (p, q, r, s) be a 4-tuple of points on a line in a projective plane, and let f be a linear fractional. Show that the cross ratio of (p, q, r, s) equals the cross ratio of (f (p), f (q), f (r), f (s)).
13. (a) [3] State a set of axioms that define a projective plane.
(b) [4] Show that every line in a projective plane contains at least 3 points.
![]()
![]()
14. (a) [2] State the Projective Desargues’ Theorem.
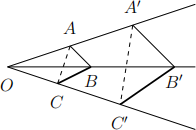
(b) [4] Suppose the six points A, B, C, A/ , B/ , C/ lie on three concurrent lines as shown
in the figure. Suppose AB is parallel to A/ B/ and BC is parallel to B/ C/ . Use the Projective Desargues’ Theorem to show AC is parallel to A/ C/ , where “parallel” is interpreted to mean “meet on the line at infinity”.
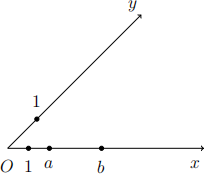
15. [5] Let a and b be two points on a line chosen to be the x-axis in a projective plane. Show that if the points ab and ba are constructed on the x-axis, then ab = ba. Be explicit about how Pappus’ Theorem gives the desired result.
16. [2] State the Three Reflections Theorem for S2 .
17. [4] Let A and B be two points of S2 . Prove that the set of points of S2 that are equidistant from A and B is a great circle.
18. [4] Use Cauchy’s Rigidity Theorem to prove that any two octahedra are congruent.
2021-12-14