ECOM044   Advanced Asset Pricing and Modelling

When writing formulas, please note the following:

O  It  is  acceptable  to  use  the  standard  alphabet  rather  than  greek  letters.   The  following  are

recommended: m for µ , s for σ, w for ω , r for ρ , d for ∆ , b for β .

O  For mathematical operators: add +, subtract -, multiply *, and divide /.         O Where appropriate, use an underscore to indicate a subscript, e.g.  r_f for rf . O  Use the ^ character for power, e.g. x^2 for x2 , x^0.5 for (x.

O  As an alternative to x^0.5 you may type sqrt(x).

O  Use brackets as necessary. To make your answer clearer use different brackets where appropriate,

e.g.  [] {}  ().

Question 1 [30 points]

Prove two no-arbitrage restrictions. The proofs should be by contradiction, that is, by assuming that the (in)equality does not hold and showing how you can then construct an arbitrage. All options are written on the same non-dividend paying stock, have the same strike price K, and have the same maturity T. The superscripts AM, EU denote that the corresponding option is American, European [Note: Make sure every step in your proof is justified.]

(a)  (20 points) 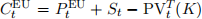 (i.e., Put-Call Parity w/o dividends), for all 0 < t, where the subscript t denotes the time at which the corresponding option/stock price is quoted.  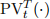is the present value operator bringing money risk-free from T to t. Explain how the Put-Call Parity is extended for a dividend paying stock.

(b)  (10 points) 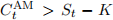 (i.e., early exercise of an American call option is never optimal on a non-dividend paying stock),  for all 0  <  t,  where the subscript t denotes the time at which the corresponding option/stock price is quoted.  Explain why the inequality you just proved does not necessarily hold.

Question 2 [35 points]

A stock price evolves in a standard binomial tree.  Each period it can either go up to u = 1.20 times its previous price or down to d = 0.90 times its previous price.  Consider a two period model (t = 0, 1, and 2), as depicted below, where each period corresponds to one year. The risk-free (net) return between t = 0 and t = 1 is r1 = 2.00%, while between t = 1 and t = 2 it is r2 = 3.00%. The initial stock price is S = 100 and the stock pays no dividends.

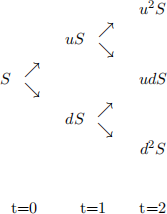
(a)  (10 points) Price an American and a European Call option on the stock with strike price K = 119

and maturity at t = 2.

(b)  (5 points) Price an American and a European Put option on the stock with strike price K = 119 and

maturity at t = 2.

(c)  (5 points) Verify that Put-Call Parity holds for the European options at t = 0 and at both nodes at t = 1. Check whether it holds for the American options.

(d)  (10 points) Price an exotic Put option with maturity at t = 2 (and no early exercise allowed) and with a strike price equal to the maximum stock price up to that point, that is, K = max}S, S1 , S2 ,, where S1  is the stock price at t = 1, and S2  is the stock price at t = 2.

(e)  (5 points) Price a derivative with maturity at t = 2, that obliges you to sell the stock at t = 2 (and

not earlier) for price max}S, S1 , S2 ,, where S1  is the stock price at t = 1, and S2  is the stock price at t = 2.