Math 454 Study Guide for the final
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Course: Math 454
Study Guide for the final
1 Concepts covered by the exam:
One-dimensional systems:
● Fixed point (equivalently, equilibrium point, or equilibrium solution).
● Phase portrait.
● Stability of fixed points: asymptotically stable (attracting) and unstable (repelling) points.
● Linear stability analysis.
● Bifurcation, bifurcation diagram.
● Blue sky (saddle-node) bifurcation.
● Transcritical bifurcation.
● Supercritical (soft) and subcritical (hard) pitchfork bifurcation.
Two-dimensional systems:
● Fixed point.
● Phase portrait, vector field.
● Linearization, Jacobian matrix, its eigenvalues and eigenvectors.
● Type and stability of a fixed point. Hyperbolic fixed points.
● Reduction of a second order ODE to a two-dimensional system.
● Conservative system, first integral (conserved quantity). Energy for an equation of type 
= j (z).
● Index of a fixed point.
● Saddle-node bifurcation.
● Node-spiral bifurcation.
● Limit cycles, stable (attracting) and unstable (repelling) limit cycles.
● Supercritical (soft) and subcritical (hard) Hopf bifurcation.
● Poincare-Bendixson theorem.
Higher-dimensional systems:
● Chaos.
2 Sample Problems
1. Consider the system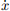 
= (x - α)(bx2 + x + b) depending on two parameters.
(a) Sketch all qualitatively different bifurcation diagrams that occur in the (b, x) plane as we vary α
(indicate stability of branches).
(b) For each fixed α, bifurcations happen for some values of ó. Sketch the dependence of those values
on α in the (a, b) plane.
(c) For each point in the graph from part (b), determine the type of the corresponding bifurcation (including which of the two pitchforks it is if it is a pitchfork).
(d) For each of the regions separated by the graph from part (b), sketch the phase portrait of the system.
2. Sketch the phase portraits of the following systems. Use the information provided by eigenvectors in the case of a saddle fixed point.
(a)
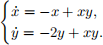
(b)
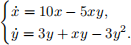
3. Consider the equation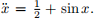 
Using conservation of energy, sketch its phase portrait in the (x, 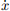) plane.
4. Consider the equation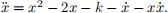 
(a) Reduce it to a 2D system.
(b) Classify the bifurcations of the system that happen as 亿 is varied.
(c) Sketch a plausible phase portrait for 亿 = 3．1.
5. Compute the indices of fixed points for the system
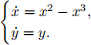
6. Show that the following system has a limit cycle for any μ ≥ 0. Find the limit cycle when μ = 0. Characterize its stability.
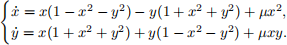
7. Explain why a 1-dimensional continuous time dynamical system cannot be chaotic.
2021-12-08