MATH10001 Graphs, Trees and Algorithms Part 1
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH10001 Mathematical Workshop
Graphs, Trees and Algorithms Part 1
Questions start on page 5
Originally of interest only to pure mathematicians, Graph Theory has be- come an important tool for applied mathematicians, biologists, economists, geographers and computer scientists. The modern computer has revolu- tionised Graph Theory by facilitating enormous experimental calculations. The most famous example of this is the Four Colour Problem, a long stand- ing mystery in mathematics that was finally solved in the 1970s, the proof relying on extensive computer calculations.
There are many everyday applications of graph theory, for example opti- mising flow through a communications network, searching a library catalogue and distributing stock across a chain of supermarket stores.
1. Definitions and Terminology
We define a graph G as a pair of finite sets V (G) and E(G), known as the vertices and the edges respectively. Each edge is given as a pair of vertices (the order of the vertices doesn’t matter here). We usually write
V (G) = {v1 , ..., vn } E(G) = {e1 , ..., ep }
where n 2 1 (p can be zero i.e. a graph can have no edges). If an edge e consists of vertices u and v we write e = uv = vu.
A diagram D(G) for G is a set of points in the plane (representing the vertices) joined by lines (representing the edges). There is no unique way to draw a diagram for a graph but all diagrams are ’topologically’ equivalent.
Example Let G have vertices {u, v, w, x, y, z} and edges {uv, uw, vw, vx, yz, xw, xy}. Then
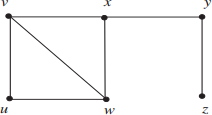
is a diagram for G.
We say two vertices are adjacent if they define an edge and that an edge is incident with its endpoints which are the defining vertices. The degree d(v) of a vertex is the number of edges that are incident with v. In the example above d(x) = 3, d(y) = 2. If d(v) is odd (resp. even) we say that v is an odd vertex (resp. even). If a vertex has degree 0 we say it is isolated.
A loop is an edge joining a vertex to itself. Any loop contributes 2 to the degree of the vertex. A graph can have multiple edges joining two vertices. If a graph has loops or multiple edges we call G a multigraph. If G has no multiple edges or loops we call G a simple graph.
A bipartite graph is one whose vertices are separated into two disjoint sets such that no two graph vertices within the same set are adjacent.
We can list the adjacency relations in an adjacency table. This lists the vertices in one column together with the vertices adjacent to them in a second column. The adjacency table for our example above is
|
u |
v, w |
|
v |
u, w, x |
|
w |
u, v, x |
|
x |
v, w, y |
|
y |
x, z |
|
z |
y |
Two graphs G and H are said to be isomorphic if their vertices can be labelled {v1 , v2 , ..., vn } and {w1 , w2 , ..., wn } so that vi and vj are adjacent in G if and only if wi and wj are adjacent in H for all 1 < i, j < n. Essentially G and H are the ’same’ graph with a relabelling of the vertices.
A path π of length m from vertex u to vertex v is a sequence of vertices (u = v0 , v1 , v2 , ..., vm = v) where vi − 1 is adjacent to vi for each i = 1, ..., m.
A closed path where the first vertex is the same as the last vertex is called a cycle.
We define the distance δ(u, v) as the minimum length of any path from u to v with δ(u, v) = o if there is no path from u to v .
We say a graph G is connected if there is a path between any pair of vertices in G. Otherwise G is disconnected.
2. Graph Algorithms
To deal with large graphs by hand or using a computer it is usual to design an algorithm to undertake a particular task. An algorithm is a finite sequence of steps with the following properties:
1. steps are followed sequentially unless a step includes an instruction for which step to perform next;
2. the instruction to stop is always reached after a finite number of steps.
In addition the algorithm has an input (in our case a description of the graph to which it applies) and an output related to the input.
Example - Breadth First Search (BFS)
This algorithm outputs the distances of all vertices v from a fixed vertex u in a graph G.
Algorithm BFS
INPUT: a graph G with root vertex u
OUTPUT: δ(u, v) for all v in G
(step 1) r := u
(step 2) i := 0 and label r with i
(step 3) find all unlabelled vertices v adjacent to a vertex with label i; if none, go to step 6
(step 4) label all vertices v of step 3 with i + 1
(step 5) i := i + 1 and go to step 3
(step 6) label all unlabelled vertices with o
(step 7) output the labelled vertices and STOP
Theorem
When BFS stops every vertex is labelled with the distance δ(u, v). Proof not included.
By the Theorem, we can use BFS to test whether a graph is connected, i.e. if BFS labels any vertex o, then the graph is disconnected.
Example
Run BFS on the following graph G with u as the root vertex.
|
s |
u, z |
|
t |
w |
|
u |
s, w |
|
v |
x |
|
w |
t, u, y, z |
|
x |
v |
|
y |
w |
|
z |
s, w |
Coursework Problems 2021 - part 1
Problem 1
A new social network has ten users and each user has ’friended’ the people they know. The list of ’friends’ for each user is as follows.
|
Name: |
|
Friends: |
|
Aleysha |
|
Devan, Hao |
|
Becki |
|
Cara, Fangyu, India |
|
Cara |
|
Becki, Fangyu |
|
Devan |
|
Aleysha, Hao |
|
Ellie |
|
Hao |
|
Fangyu |
|
Becki, Cara, George, India, Jack |
|
George |
|
Fangyu, India |
|
Hao |
|
Aleysha, Devan, Ellie |
|
India |
|
Becki, Fangyu, George, Jack |
|
Jack |
|
Fangyu, India |
Model this social network with a graph.
George is ’connected’ to Becki indirectly, for example George → India → Becki. List all the ways that Cara can be connected to Jack via exactly one or exactly two other people.
Name two people who can not be connected.
Create a table showing the ’degree’ of each vertex in your graph. What do you notice about the sum of all the degrees? Why is this?
Problem 2
The complete graph Kn on n vertices is such that every pair of vertices is joined by a single edge. Draw diagrams for Kn for n = 2, ..., 6. Write down a formula for the sum of the degrees of the vertices in Kn for any n 2 1. Use induction on n to prove your formula holds for all n 2 1. Explain why any diagram for K5 drawn in the plane must have two edges that cross.
Problem 3
(i) Draw a diagram for the graph whose adjacency table is
|
a |
b |
|
b |
a, c, d |
|
c |
b, e |
|
d |
b, f, g |
|
e |
c |
|
f |
d, g |
|
g |
d, f |
Is the graph bipartite? Give a reason for your answer.
(ii) Run Algorithm BFS on this graph with a as the root. Write out all the steps in the algorithm.
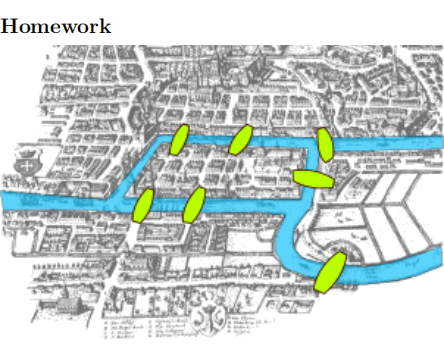
In 1735 Leonhard Euler used graph theory to solve the ’Bridges of K¨onigsberg’ problem. K¨onigsberg had four land masses joined by seven bridges as in the picture above. People wanted to know if it was possible to take a circular walk that crossed every bridge exactly once.
Briefly explain, in your own words, how Euler could have modelled this problem using a graph and how he could have solved the problem.
2021-12-01