闪电代写 -代写CS作业_CS代写_Finance代写_Economic代写_Statistics代写_代码代做_IT代写_加急帮助

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

EECS 325 – Fall 2021

Analysis of Algorithms

Homework 4

Instructions:

● This homework is due by 11:59PM Paciﬁc Time on Thursday, December 2nd. You have a one-time grace period allowing you to submit a homework assignment up to two days late. Subsequent assignments submitted up to two days late will incur a 20% penalty. Assignments submitted more than two days late will not be graded and will receive a score of 0.

● You must submit your written solutions as a single .pdf ﬁle on Canvas with your name at the top. Typesetting your written solutions using LATEX is strongly encouraged. If you solve the extra credit part of Question 1 you must submit your solution as a single .cpp, .java, or .py ﬁle depending on your choice of language.

● You are welcome and encouraged to discuss the problems in groups of up to three people, but you must write up and submit your own solutions and code. You must also write the names of everyone in your group on the top of your submission.

● The primary resources for this class are the lectures, lecture slides, the CLRS and Erickson algorithms textbooks, the teaching staﬀ, your (up to two) collaborators, and the class Piazza forum. We strongly encourage you only to use these resources. If you do use another resource, make sure to cite it and explain why you needed it.

● Scoring: 50 points with up to 5 points of extra credit.

Question 1 (Chomping logs, 12 points + 5 extra credit points). Filbert and Maple are beavers at the Oregon Zoo. They are experts at chomping logs into pieces, and, realizing that there’s a market for logs of a particular length, they decide to monetize their skills. In this problem you will design an algorithm to help Filbert and Maple maximize their proﬁt.

As input, you get an integer L > 1 corresponding to the length of the starting log to be chomped (in feet), and a table corresponding to the retail value v(i) of i-foot-long logs for each integer 1 < i < L. The goal is to pick a number of pieces k satisfying 1 < k < L and integer lengths e1 , . . . , ek satisfying 1 < e1 < . . . < ek < L so that L = i(k)=1 ei (the sum of the lengths of the log pieces is equal to the length of the original log) and the total retail value i(k)=1 v(i) is maximized

over all choices of k and e1 , . . . , ek. The ﬁnal output is the maximum possible total retail value i(k)=1 v(i).

Consider the example in the following table:

a. (8 points) Design a tabulation-based dynamic programming algorithm for solving the “chomping logs” problem. Give pseudocode for your algorithm and analyze its runtime. Clearly specify what the dimensions of your table are, what each entry in the table represents, and how the value of each in the table is computed.

(Hint: Suppose that you were given the value of e_ . How could you use that to help solve the problem?)

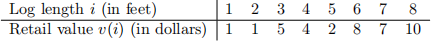
Table 1: An input table of log retail values v(i). If L = 8, then by picking k = 3, e1 = 1, e2 = 1, e3 = 6, we get that i(k)=1 ei = 1 + 1 + 6 = 8 = L, as required, and that the total retail value with these choices is i(k)=1 v(ei) = v(1) + v(1) + v(6) = 1 + 1 + 8 = 10. Alternatively, we could have achieved the same total value by picking k = 1, e1 = 8 for a total value of i(1)=1 v(ei) = v(e1 ) = v(8) = 10. In part (b), you will analyze whether it’s possible to do better.

b. (4 points) Show the dynamic programming table produced by your algorithm from part (a) when the starting log has length L = 8 and log retail values are as speciﬁed in Table 1. Also state the ﬁnal answer.

c. (5 points extra credit) Implement your algorithm from part (a). Your program should take a ﬁle name as input. The ﬁle should contain the values v(1), . . . , v(L) in order from, separated by single spaces (the values i in the top row of the input table and the value of L are implicit from this information). Your program should output a single number corresponding to the maximum possible total retail value.

For example, on input

4 8 3 8 9

corresponding to the values of v(1), v(2), v(3), v(4), v(5) your program should output

d. (0 points but highly recommended.) Watch videos of Filbert and Maple (https://www.youtube. com/watch?v=6_idLrnt6vQ) and of Filbert in full log-chomping action (https://www.youtube. com/watch?v=uWwtKXoQKZA).

Question 2 (3-SAT to Exact-3-SAT, 12 points). Recall that in class we deﬁned 3-SAT as the variant of CNF-SAT where each clause contains lu motu 3 literals (i.e., a clause may contain 1, 2, or 3 literals). Deﬁne Exact-3-SAT to be the variant of CNF-SAT where each clause contains dαlauly 3 literals. Prove that Exact-3-SAT is NP-complete.

a. Prove that Exact-3-SAT is in NP.

(Hint: Give a polynomial-time veriﬁer. Make sure to state what information is contained in the certiﬁ- cates that make it accept on YES instances. The veriﬁer and certiﬁcates should be very similar to the ones for 3-SAT.)

b. Give a polynomial time reduction from 3-SAT to Exact-3-SAT. Conclude that Exact-3-SAT is NP-hard, and by part (a), also NP-complete.

(Hint: Start by thinking about the special case where the input CNF-SAT formula consists of just one clause C. If C contains only one or two literals, show how to reduce it to an equisatisﬁable Exact-3-SAT formula (potentially containing new variables and more than one clause).)

Question 3 (Search-to-decision reduction for 3-SAT, 12 points). Suppose that you have a polynomial- time algorithm D for deciding whether a 3-SAT formula Φ(x1 , . . . , xn) on n variables is satisﬁable. Design a polynomial-time algorithm that, when given a satisﬁable such formula Φ as input, uses D as a “black-box” subroutine to ﬁnd a Boolean assignment a1 , . . . , an e {0, 1} that satisﬁes Φ (i.e., an assignment so that Φ(a1 , . . . , an) = 1).1

(Hint: Note that D outputs one bit of information each time you query it. How many bits of information does a satisfying assignment to Φ consist of?)

Question 4 (Guards and Streets, 14 points). The GuARDsANDSTREETs Problem is the decision problem deﬁned as follows. As input, you are given a set of locations L = {e1 , . . . , en}, a set of streets S = {s1 , . . . , sm}, and a number k > 0 as input. Each street s has exactly two distinct locations ei and ej as its endpoints. Each location may be the endpoint of any number of streets, and a guard can be stationed (or not) at each location. A street s e S is called gzlscdc if a guard is stationed at at least one of its endpoints, and S is called uoullly gzlscdc if each street s e S is guarded. The goal of the problem is to decide whether:

● (YES instances) It is possible to totally guard S using g < k guards.

● (NO instances) To totally guard S, it is necessary to use g > k guards.

a. (4 points) Prove that the GuARDsANDSTREETs Problem is in NP.

(Hint: Give a polynomial-time veriﬁer. Make sure to state what information is contained in the certiﬁ- cates that make it accept on YES instances.)

b. (10 points) Give a polynomial-time reduction R from the INDEPENDENTSET Problem that we saw in class to the GuARDsANDSTREETs Problem. Conclude that the GuARDsANDSTREETs Problem is NP-hard, and by part (a), also NP-complete.

(Hint: Model the GuARDsANDSTREETs Problem as a graph problem. Make sure to show that your reduction maps YES instances of the INDEPENDENTSET Problem to YES instances of the GuARD- sANDSTREETs Problem, and NO instances of the INDEPENDENTSET Problem to NO instances of the GuARDsANDSTREETs Problem.)

1 The algorithm you are asked to design in Question 3, where you are using a black-box algorithm for one problem to solve another, is actually a type of reduction. These reductions are a bit diﬀerent from the ones that we saw in class for reducing instances of decision problems to equisatisﬁable instances of other decision problems. That type of reduction from class is called a mapping reduction, and the type of reduction in this problem is called a Turing reduction.