Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MAT244: Introduction to Ordinary Differential Equations

Fall 2021

Homework 5

1 Problems to be submitted

1. For each of the following 3 × 3 matrices compute the geometric and the algebraic multiplicity of their eigenvalues.

(a) (2 points)

(b) (4 points)

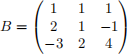
(c) (4 points)

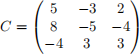
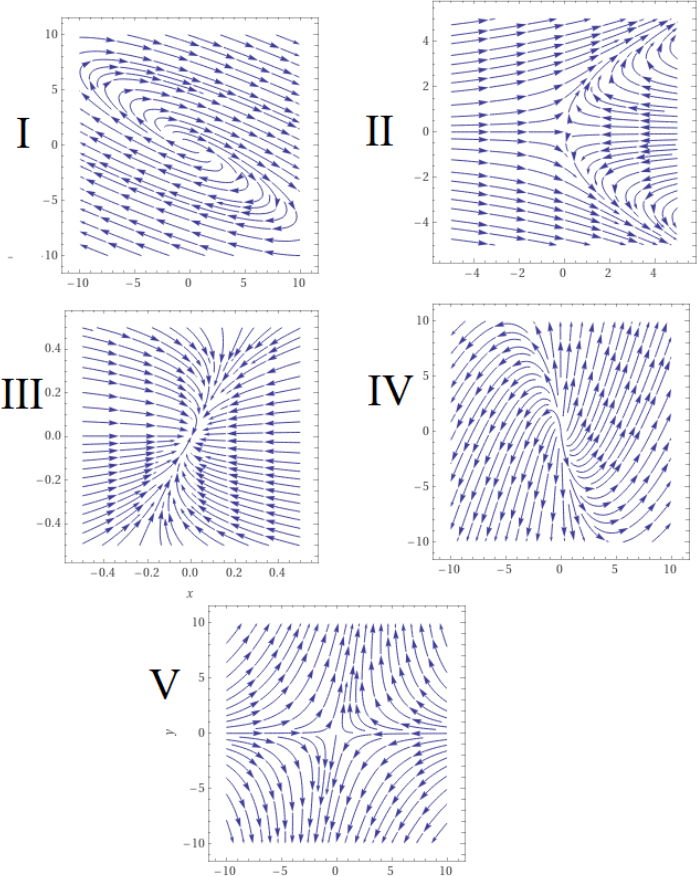
2. The figure in the next page shows the phase diagram of 5 plane systems. Exactly one of them is nonlinear. Of the remaining four, exactly one is a nondiagonalizable one and the rest are diagonalizable.

(a) (5 points) Identify the nondiagonalizable one and the nonlinear one. Explain your answer.

(b) (5 points) For the 3 systems that are diagonalizable decide whether the eigenvalues are: two positive real numbers, two negative real numbers, one positive and one negative real number or a complex pair. Explain your choice carefully.

3. Solve the initial value problem

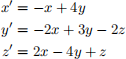
with x(0) = 1, y(0) = 1, z(0) = 1 by following the next steps:

(a) (2 points) By finding the geometric and algebraic multiplicities of the eigenvalues of the associated matrix verify that the homogeneous system is diagonalizable.

(b) (2 points) Find a basis of eigenvectors for the associated matrix, that is, for

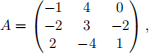
and use it to construct a matrix P such that  AP is diagonal.

(c) (3 points) Compute the exponential . [Hint: Use the previous part to simplify your computa-tions].

(d) (3 points) Use all the preivous parts to compute the answer to the initial value problem.

4.       (a) (4 points) A particle moves in the plane with a curve describing its motion of the form (x(t), y(t)). If its velocity vector at each point of time coincides with (y(t), x(t)), find the equations describing its movement.

(b) (6 points) A particle moves in the plane with a curve describing its motion of the form (x(t), y(t)). If its acceleration vector at each point of time coincides with (y(t), x(t)), find the equations describing its movement. [Hint: to get rid of the second derivatives introduce new variables.]

5. (10 points) For t > 0 and an invertible matrix A of n × n consider the system

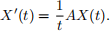
This is not a constant coefficient linear system due to the appearance of the factor 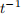on the right hand side. We explore how to solve this system for some cases now.

(a) (3 points) Just as we did in lecture for the constant coefficient case, we suggest a solution of a certain form and see what do we need for it to work. In this case we suggest

for some fixed vector v and real number r. Verify this is a solution to this system if and only if r is an eigenvalue of A and v is an eigenvector for r.

(b) (4 points) Suppose A is a diagonalizable matrix with (possible repeated) real eigenvalues r1, ..., rn and a basis of corresponding eigenvectors v1, ..., vn. Jutify that the solutions found in part (a), that is,

are a fundamental system of solutions. [Hint: Prove they are linearly independent by writing a linear combination and evaluating at a convenient value of t.]

(c) (3 points) Find the general solution to the following system

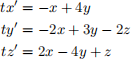
[Hint: You already found the associated matrix in problem 3.]