Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MATH3306: Set Theory and Mathematical Logic

Semester Two Final Examination, 2020

1. (10 marks)

Construct a deterministic finite state automaton that for the alphabet {a, b, c} recognises all words that

● begin with an ab,

● end with an a,

● do not contain either bb, cc, or cb, and

● between any two c’s, there is at least one b.

For example, this will accept aba, abca, and abaabcabcaaa but reject ε (the empty word), aca, abba, abcaaca, abcca, and abacbaca. Give your finite state automaton as a diagram using circles for states and arrows for transitions.

2. (10 marks)

For the input alphabet {a, b}, construct a deterministic Turing machine that recognises the language

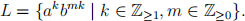
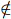Give your Turing machine as a diagram using circles for states and arrows for transitions. (So it should accept aa L and aaabbbbbb L, but reject aab L and the empty word.) Sketch how the Turing machine works, but you do not have to prove it.

3. (10 marks)

For the alphabet {a, b}, prove that no deterministic FSA can recognise the language

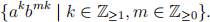
4. (10 marks)

The number of integer partitions of n with largest part k, or the number of ways to write n as a sum of integers in {1, 2, . . . , k} (up to reordering), can be constructed recursively by

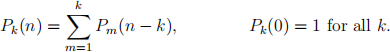
Prove that Pk(n): N → N is primitive recursive for any fixed k.

5. (10 marks)

The running time of a (numerical) Turing machine on input x is the number of steps the Turing machine performs before it halts. We are going to construct a partial function f(a, b, x) as follows. If either a, b ∈ N is not the  number of a Turing machine, then f(a, b, x) is undefined. Otherwise, let Ta and Tb be the corresponding Turing machines. In this case, we define

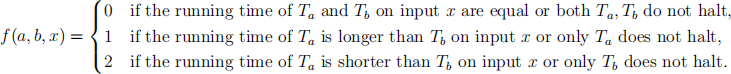
Show that f is not a partial recursive function.

Hint: Use the undecidability of the halting problem and fix a particular Turing machine Tb.

6. (5 marks each; 10 marks total)

(a) How many isomorphisms from the ordinal h  into itself exist? Justify your answer with a proof.

(b) Determine whether the real intervals (0, 1) and [2, 3] with their usual ordering are isomorphic to an ordinal. Justify your answer with a proof.