Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

CS 344

Problem Set 3

Fall 2021

        Honor Code: Students may discuss and work on homework problems in groups, which is encouraged. However, each student must write down their solut ions independently to show they understand the solution well enough to reconstruct it by themselves. Students should clearly mention the names of the other students who offered discussions. We check all submissions for plagiarism. We take the honor code seriously and expect students to do the same.

        Instruction for Submission: This homework has a total of 100 points (+10 bonus points), it will be rescaled to 10 points (+1 bonus point) as the eventual score. We encourage you to use LaTex to write your answer, because it’s particularly suitable to type equations and it’s frequently used for writing academic papers. We have provided the homework3.tex file for you, you can write your answer to each question in this .tex file directly after the corresponding question, and then compile the .tex file into a PDF file for submission. As a quick introduction to LaTex, please see this Learn LaTeX in 30 minutes . Compiling a .tex file into a PDF file needs installing the LaTex software on your laptop. It’s free and open source. But if you don’t want to install the software, you can just use this website https://www.overleaf.com/, which is also free of charge. You can just create an empty project in this website and upload the homework1.zip, and then the website will compile the PDF for you. You can also directly edit your answers on the website and instantly compile your file.

        You can also use Microsoft Word or other software if you don’t want to use LaTex. If so, please clearly number your answers so that we know which answer corresponds to which question. You also need to save your answers as a PDF file for submission.

        Finally, please submit your PDF file only. You should name your PDF file as “Firstname-Lastname-NetID.pdf’’.

        Late Policy: The homework is due on 11/22 (Monday) at 11:59pm. We will release the solutions of the homework on Canvas on 11/26 (Friday) 11:59pm. If your homework is submitted to Canvas before 11/22 11:59pm, there will no late penalty. If you submit to Canvas after 11/22 11:59pm and before 11/26 11:59pm (i.e., before we release the solution), your score will be penalized by 0.9k , where k is the number of days of late submission. For example, if you submitted on 11/25, and your original score is 80, then your final score will be 80 ∗ 0.93 = 58.32 for 25 − 22 = 3 days of late submission. If you submit to Canvas after 11/26 11:59pm (i.e., after we release the solution), then you will earn no score for the homework.

Drawing graphs: You might try http://madebyevan.com/fsm/ which allows you to draw graphs with your mouse and convert it into LATEX code:

        You can also draw by hand and insert a picture.

        Make best use of picture in Latex: If you think some part of your answer is too difficult to type using Latex, you may write that part on paper and scan it as a picture, and then insert that part into Latex as a picture, and finally Latex will compile the picture into the final PDF output. This will make things easier. For instructions of how to insert pictures in Latex, you may refer to the Latex file of our homework 1, which includes several examples of inserting pictures in Latex.

1. Warmup with DFS/BFS. (20 points)

(1) Give one example of a directed graph on four vertices, A, B, C, and D, such that both depth-first search and breadth-first search discover the vertices in the same order when started at A.

(2) Give one example of a directed graph where DFS and BFS discover the vertices in a different order when started at A.

“Discover” means the time that the algorithm first reaches the vertex, referred to as start_time during lecture. Assume that both DFS and BFS iterate over outgoing neigh-bors in alphabetical order.

[We are expecting a drawing of your graphs and an ordered list of vertices discovered by DFS and BFS.]

2. Warmup with Dijkstra. (25 points)

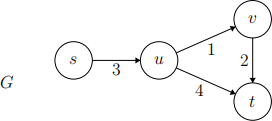
Let G = (V, E) be a weighted directed graph. For the rest of this problem, assume that s, t ∈ V and that there exists a directed path from s to t.

For the rest of this problem, refer to the implementation of Dijkstra’s algorithm given by the pseudocode below.

dijkstra_st_path(G, s, t):

    for all v in V, set d[v] = Infinity

    for all v in V, set p[v] = None

    // we will use p to reconstruct the shortest s-t path at the end

    d[s] = 0

    F = V

    D = []

    while F isn’t empty:

        x = vertex v in F such that d[v] is minimized

        for y in x.outgoing_neighbors:

            d[y] = min( d[y], d[x] + weight(x,y) )

            if d[y] was changed in the previous line, set p[y] = x

        F.remove(x)

        D.add(x)

    // use p to reconstruct the shortest s-t path

    path = [t]

    current = t

    while current != s:

        current = p[current]

        add current to the front of the path

    return path, d[t]

The variable p maintains the “parents” of the vertices in the shortest s-t path, so it can be reconstructed at the end.

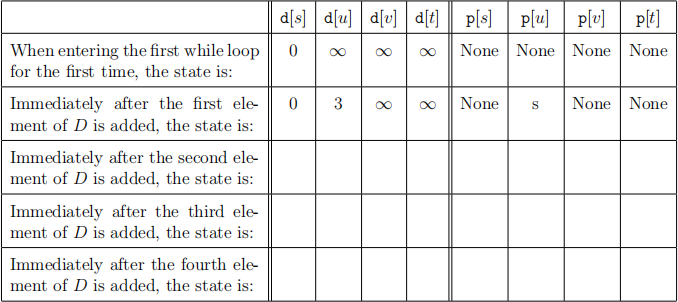
Step through dijkstra_st_path(G, s, t) on the graph G shown below. Complete the table below to show what the arrays d and p are at each step of the algorithm, and indicate what path is returned and what its cost is.

[We are expecting the table below filled out, as well as the final shortest path and its cost. No further justification is required.]

3. Fun with Reductions. (15 points) Suppose the economies of the world use a set of currencies C1, . . . , Cn; think of these as dollars, pounds, Bitcoin, etc. Your bank allows you to trade each currency Ci for any other currency Cj, and finds some way to charge you for this service. Suppose that for each ordered pair of currencies (Ci, Cj), the bank charges a flat fee of fij > 0 dollars to exchange Ci for Cj (regardless of the quantity of currency being exchanged).

Describe an algorithm which, given a starting currency Cs, a target currency Ct, and a list of fees fij for all i, j ∈ {1, . . . , n}, computes the cheapest way (that is, incurring the least in fees) to exchange all of our currency in Cs into currency Ct. Also, justify the its runtime.

[We are expecting a description or pseudocode (either is OK) of your algo-rithm, as well as a brief justification of its runtime. You can use any algorithm we have learned in class.]

4. Social engineering. (20 points)

Suppose we have a community of n people. We can create a directed graph from this community as follows: the vertices are people, and there is a directed edge from person A to person B if A would forward a rumor to B. Assume that if there is an edge from A to B, then A will always forward any rumor they hear to B. Notice that this relationship isn’t symmetric: A might gossip to B but not vice versa. Suppose there are m directed edges total, so G = (V, E) is a graph with n vertices and m edges.

Define a person P to be influential if for all other people A in the community, there is a directed path from P to A in G. Thus, if you tell a rumor to an influential person P, eventually the rumor will reach everybody. You have a rumor that you’d like to spread, but you don’t have time to tell more than one person, so you’d like to find an influential person to tell the rumor to.

In the following questions, assume that G is the directed graph representing the commu-nity, and that you have access to G as an array of adjacency lists: for each vertex v, in O(1) time you can get a pointer to the head of the linked lists v.outgoing_neighbors and v.incoming_neighbors. Notice that G is not necessarily acyclic. In your answers, you may appeal to any statements we have seen in class, in the notes, or in CLRS.

(a) (10 points) Show that all influential people in G are in the same strongly connected component, and that everyone in this strongly connected component is influential.

[Hint: You need to refer the definition of strongly connected component, and you can prove using either induction or contradiction.]

(b) (10 points) Suppose that an influential person exists. Give an algorithm that, given G, finds an influential person.

[We are expecting a description or pseudocode of your algorithm and a short argument about the runtime. You can borrow any algorithm that we have learned in class.]

5. Job Sequencing Problem. (10 bonus points)

In this problem we have n jobs j1, j2, ..., jn, each has an associated deadline d1, d2, ..., dn and profit p1, p2, ..., pn. Profit will only be awarded or earned if the job is completed before the deadline. We assume that each job takes 1 unit of time to complete. The objective is to earn maximum profit when only one job can be scheduled or processed at any given time.

Describe or provide the pseudocode of an algorithm to find the sequence of jobs to do with the maximum total profit.

[Hint: You can select the jobs in a greedy way. You can use the following example to help your analysis.]

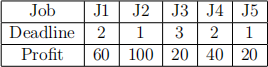
The best job sequence would be J2 → J1 → J3.

6. Alternative Minimum Spanning Trees (23.4 CLRS). (20 points) In this problem, we give pseudocode for two different algorithms. Each one takes a connected graph and a weight function as input and returns a set of edges T. For each algorithm, either show that T is a minimum spanning tree (give a brief justification of the algorithm) or show that T is not a minimum spanning tree (give a counter-example).

a. (10 points) MAYBE-MST-A (G, w)

1. sort the edges into non-increasing order of edge weights w

2. T = E

3. for each edge e ∈ E, taken in non-increasing order by weight

4. if T − {e} is a connected graph

5.    T = T − {e}

6. return T

b. (10 points) MAYBE-MST-B (G, w)

1. T = null

2. for each edge e, taken in arbitrary order

3.   if T ∪ {e} has no cycles

4.    T = T ∪ {e}

5. return T