EE575: HOMEWORK 2 (DUE 02/13/2020)
Problem 1. Simulate 1D metal rod of unit length. Use 1D assumptions (constant temperature across crossection etc). Initial temperature f(x,0) =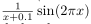 boundary conditions f(0,t) = f(L,t) = 0. Run the heat equation and plot the temperature as a function of time. (Hint: Refer to the handout posted on blackboard for some useful source code). (10pt)
boundary conditions f(0,t) = f(L,t) = 0. Run the heat equation and plot the temperature as a function of time. (Hint: Refer to the handout posted on blackboard for some useful source code). (10pt)
Problem 2. Simulate 2D unit square plate using a 256x256 regular grid, with initial temperature f(x,y,t = 0) = sin(2πx)cos(2πy). Assume the Dirichlet boundary conditions of 0 temperature on the boundary. Run the heat equation and plot the temperature distribution as a function of time. Take any black and white 256x256 image and run the heat equation on the intensity values. Show the smoothing behavior of the heat equation. (Extra credit (2pt): Create a movie showing heat change over a period of time). Hint: Check delsq function in matlab. (10pt)
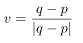
and show that
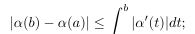
that is, the curve of shortest length from α(a) to α(b) is the straight line joining these points.
Problem 4. (2pt) The trace of the parameterized curve (arbitrary parameter) α(t) = (t,cosht), t ∈ R, is called catenary. Show that the signed curvature of the catenary is
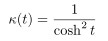 .
.
Problem 5. (4pt) Plot the Frenet frame for a regular parameterized curve for (tcos(6t),tsin(6t),t). You can write your own code or use the Matlab code that I wrote as a starting point available on blackboard.
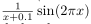 boundary conditions f(0,t) = f(L,t) = 0. Run the heat equation and plot the temperature as a function of time. (Hint: Refer to the handout posted on blackboard for some useful source code). (10pt)
boundary conditions f(0,t) = f(L,t) = 0. Run the heat equation and plot the temperature as a function of time. (Hint: Refer to the handout posted on blackboard for some useful source code). (10pt)Problem 2. Simulate 2D unit square plate using a 256x256 regular grid, with initial temperature f(x,y,t = 0) = sin(2πx)cos(2πy). Assume the Dirichlet boundary conditions of 0 temperature on the boundary. Run the heat equation and plot the temperature distribution as a function of time. Take any black and white 256x256 image and run the heat equation on the intensity values. Show the smoothing behavior of the heat equation. (Extra credit (2pt): Create a movie showing heat change over a period of time). Hint: Check delsq function in matlab. (10pt)
Problem 3. (4pt) (Straight Lines as Shortest) Let α : I → R 3 be a parameterized curve. Let [a,b] ⊂ I and set α(a) = p, α(b) = q. a. (2pt) Show that, for any constant vector v, |v| = 1,
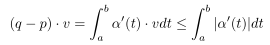
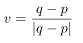
and show that
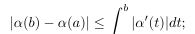
that is, the curve of shortest length from α(a) to α(b) is the straight line joining these points.
Problem 4. (2pt) The trace of the parameterized curve (arbitrary parameter) α(t) = (t,cosht), t ∈ R, is called catenary. Show that the signed curvature of the catenary is
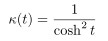 .
.Problem 5. (4pt) Plot the Frenet frame for a regular parameterized curve for (tcos(6t),tsin(6t),t). You can write your own code or use the Matlab code that I wrote as a starting point available on blackboard.
2020-02-06