Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MATH268:Assignment 3 - Dynamic Programming

Exercise 1 At each play of the game, a gambler can bet any nonnegative amount up to his present fortune and will either win or lose that amount with probability p ∈ (0, 1) and 1 − p, respectively. By saying “win that amount”, we mean he gets a net profit of ”that amount”. The gambler is allowed to make n bets, and his objective is to maximize the expectation of the logarithm of his final fortune. What strategy achieves this end when p ≤ 1/2? What is the optimal value of this problem if the gambler has initial fortune x > 0?

Exercise 2 Let Sk denote the price of a given stock on the kth day (k ≥ 1) and suppose that

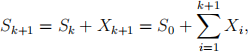
where X1, X2, . . . are i.i.d. with common distribution function F. Assume X1, X2, . . . are independent on S0 (the initial price), and the mean E[Xi] := µF < 0, i = 1, 2, · · · is finite. (We allow the “stock” price to fall below 0.)

        Suppose that you own an option to buy one share of the stock at a fixed price, say c, and you have N days in which to exercise the option. You are not obliged to exercise it, but if you do at a time whe n the stock’s price is s, then your profit is s − c (i.e., buy a share of stock at c and immediately sell it at the price s). You are interested in the policy maximizes your expected profit.

(a) Write down the optimality equation. (You may formulate a suitable dynamic programming problem with the following meaning of states: sn is the stock price, and the option has not been exercise, at the day n.)

(b) Prove that Vn(s) − s is decreasing in s.

(c) Show that one can take an optimal policy in the following form: there is an increasing sequence of numbers b1 ≤ b2 ≤ b3 ≤ · · · ≤ bn ≤ . . . such that if there are n days to go, and the present price is s, then one should exercise the option if s ≥ bn and not exercise if s < bn. (You may use the fact that Vn(x) is continuous in x without justifications.)