❼ This assignment is assessed. Your work for this assignment must be submitted by 2pm on Friday April 19, 2024.

❼ You are only required to submit your scanned answer online. Only electronic sub-mission is acceptable.

–  Remember also to write down your name and student number in the answer document. The submission of your answer should be done via LMS over the Assignment 1 Upload Point under the Assignments folder. Only 1 single PDF document would be accepted. The PDF file should be save as "your  student ID [Your name]. pdf", fail to meet this requirement would not be accepted. In additional, no any other format, including any photo format, would be accepted except PDF format.

– It is preferred that your submission typed, but if it is handwritten, make sure that it is neat and legible. To ensure your working is clear and legible, you should use a black or blue pen and light coloured (white) paper. Your name and student ID should be on every page and pages should be numbered. Your scanned working should be in PDF format with pages stitched together.

❼ This assignment counts for 10% of your final marks for STAT3061.

❼ Please ensure that you write your name and student number on your work.

❼ You must demonstrate appropriate method and reasoning. Correct answers may not necessarily earn full marks if they do not demonstrate an appropriate level of understanding of the concepts and methods required.

❼ You may use R or any other computational software for matrix operations and for solving systems of equations. When referring to such software in your answers, please include the relevant output and the source code used.

❼ Unless special considerations were granted, any student failing to submit work by the deadline will receive a penalty for late submission (5% per day late, 0 marks after 7 days). The number of days late by is a whole number rounded up from the time after 2pm on the due date.

❼ Plagiarism:  The work that you submit must be your sole effort (i.e. not copied from someone else). If you are found guilty of plagiarism, you will be subjected to disciplinary action. You are reminded of the University ‘Policy on Plagiarism’:

Questions

1.  [14 marks] The board for a modified Snakes and Ladder game is shown below.

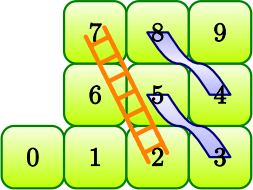
This game uses a tetrahedron (four-faced) die, numbered {1, 2, 3, 4}. We’ll represent the player’s position at anytime nas Xn. It’s a single-player game starting at square 0. Rolling the die moves you forward by the number shown. If your piece lands at the base of a ladder, you climb to the top. But if it lands at the head of a snake (or the top of a chute here), you slide down to its tail. There’s a special rule: If your roll goes past the last square (square 9), you stay in your current position. For instance, if you’re at square 6 and roll a 4, you don’t move and stay at square 6.

(a)  [2 marks] State the state space of (Xn  : n ≥ 0).

(b)  [4 marks] Determine the transition probability matrix.

(c)  [4 marks] Draw the transition diagram of the transition probability matrix.

(d)  [4  marks] Let the game start at square 0, i.e., X0  = 0. Find the expected length of the game.

2.  [12  marks] Consider the experiment of tossing a coin until the pattern HTH is obtained. Assume that P(H) = p and P(T) = q = 1 − p.

(a)  [4 marks] Construct the Engel diagram for the experiment. You must include in your graph the direction and the probabilities.

(b)  [6 marks] Obtain the equations solution of which will help find the expected waiting time for the HTH pattern.

(c)  [2 marks] Find the expected waiting time for the HTH pattern.

3.  [22 marks] A production line comprises three machines working independently of each other. For each machine, the probability of working through the day isp ∈ (0, 1) and may breakdown during a day with probability q = 1 − p, independently of its previous history. There is a single repairman who, if he has to, repairs exactly one machine overnight. If there is a machine not working by the end of the day, then the repairman works during the night and it is guaranteed to work by the morning. Let Xn denote the number of working machines at the end of day before the repairman begins any over-night repair.

(a)  [2 marks] Specify the state space of (Xn  : n ≥ 0).

(b)  [2  marks]  Determine the transition  matrix in terms of p  (some reasoning should be given).

(c)  [2 marks] Given that 2 machines are idle tonight, what is the probability of one idle machine 3 nights later, if p = 0.8 (answer 6 decimal places).

(d)  [5 marks] Present the transition diagram of transition matrix from part (b), find the period of each state.

(e)  [3 marks] For each state, decide whether it is recurrent or transient.

(f)  [4  marks] Compute the expected hitting time of state 3 starting from each state.

(g)  [4 marks] Determine the stationary distribution for the Markov chain

4.  [16  marks] Consider a Markov chain with state space  {1, 2, 3, 4} and transition matrix P given below:

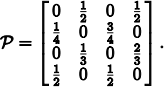
(a)  [4 marks] Find the period of each state.

(b)  [4 marks] For each state, decide whether it is recurrent or transient.

(c)  [4  marks] Compute the expected hitting time of state 3 starting from each state.

(d)  [4 marks] Determine the stationary distribution for the Markov chain

5.  [12  marks]  For each of the matrices given below, decide whether it could be a transition matrix. In each case, justify your decision.