Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MATH 526: Homework 3

Fall 2021

Instructions

● Each homework submission must be a single pdf file containing all derivations in the order they were assigned.

● Any derivations or comments can be written in Latex or be photos of neatly handwritten work.

● All results have to be justified by appropriate intermediate steps or arguments to receive full credit.

1. Find the discounted expected payoff of each pure stationary control in the following MDP, and deter-mine the discounted value for each discount factor. The state space is {s1, s2}; the action set is {u, d}; the payoff function is

and the transition probabilities are

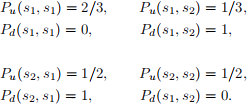
This information is summarized in the table below.

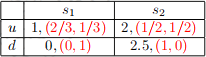
Hint: to find the value function draw the discounted expected cost for each of the pure stationary controls on the same plot. You may use Matlab, or any graphing calculator for this purpose. For comparison between the expectations, multiply each by

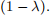
(25 points)

2. Recall the example from the notes: In a hardware store you must first go to server 1 to get your goods and then go to a server 2 to pay for them. Suppose that the times for the two activities are exponentially distributed with rates λ (station 1) and µ (station 2). We already computed the expected amount of time it takes Bob to get his goods and pay if when he comes in there is one customer named Aniyah with server 1 and no one at server 2.

Now, we solve the following questions. Suppose that when Chun reaches station 1, Bob is right in front of her in Station 1, and Aniyah waits in station 2. Assume that there are queues for both stations. That is, if Bob finishes service in station 1 before Aniyah finishes here service in station 2, then Bob waits in the queue of station 2 and Chun enters service in station 1.

(a) What is the expected time until Chun finishes both services?

(b) In this part assume that Bob and Aniyah do not get along, so that if Bob finishes his service before Aniyah, then he leaves the store. Calculate now the expected time it takes Chun to finish her services.

(12 + 13 = 25 points)

3. Bill assembles toys in a factory. The assembly time of each toy is exponentially distributed with mean of 6 minutes, independently of previous assembles.

(a) What is the probability that the assembly time of the fourth toy is less than 6 minutes?

(b) For each toy that Bill assembles in less than 6 minutes, Bill receives a bonus. What is the the expected number of bonuses that Bill receives among the 100 toys?

(c) Bill’s daughter arrives at the factory an hour after Bill starts working. She stays there for either 2, 3, or 4 minutes, with probability 1/3, each (independently of her dad’s progress). What is the probability that she will see her dad finishes assembling a toy, while she is there?

(d) Assume that with probability 1/10 Bill assembles a toy incorrectly, independently of previous assemblies. Given that in the first hour there is exactly one toy that Bill assembled incorrectly, what is the probability he assembled a total of 10 toys in the first hour and 10 toys in the next hour?

(e) What is the distribution of the number of toys that Bill managed to assembled in the first 20 minutes, if it known that at time t = 0 Bill started working, and within the first hour, Bill assembled 15 toys?

(f) What is the expectation of the number of toys that Bill managed to assembled in the first 20 minutes, if it known that at time t = 0 Bill started working, and between minute 10 and 60 Bill assembled 15 toys?

(4 + 4 + 4 + 4 + 4 + 5 = 25 points)

4. (2.54 in Durrett) Let St be the price of stock at time t and suppose that at times of a Poisson process with rate λ the price is multiplied by a random variable Xi > 0 with mean µ and variance σ² . That is,

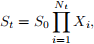
where the product is 1 if Nt = 0. We assume that X0 is deterministic and {Xn}n is a sequence of independent r.v.’s and independent of the Poisson process N. Find E[St] and Var(St).

(25 points)