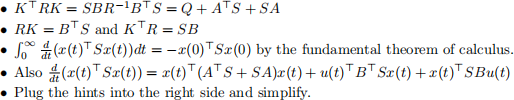EE 4233 - Spring 2023 Exam 2
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
EE 4233 - Spring 2023
Exam 2
This exam has 3 questions each with 3 parts. Each part is worth 10 points. Show all your work. Answers without work or explanation may lose credit.
Problem 1: Final Values and Other Asymptotic Analysis
a: Let  Calculate limt→∞ x(t).
Calculate limt→∞ x(t).
b: Let
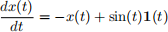
where 1(t) is the unit step. Calculate lims→0 sX(s), and explain why this is not equal to limt→∞ x(t).
c: Consider a single-input/single-output linear system:

and u(t) is generated by an integral controller:
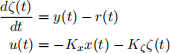
where r(t) is a reference signal.
Assume that r(t) is the unit step and the eigenvalues of
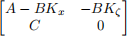
have negative real-parts. Calculate limt→∞ x(t) and limt→∞ ζ(t).
Problem 2: State Feedback Design
a: Let A and B be given by

Find a gain vector, K = [K0 K1], such that A − BK has eigenvalues −1 and −2.
b: Find the gain K such that u(t) = −Kx(t) solves the linear quadratic regulator problem

with

Hint: A − BK must have negative real-part eigenvalues.
c: Say that
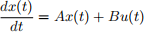
and S satisfies
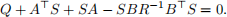
Show that if limt→∞ x(t) = 0 and K = R−1B> S, then
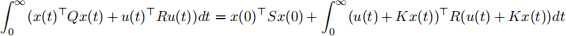
Hints:
Problem 3: Observers
a: Let A and C be given by
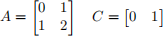
Find a gain vector, 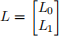 , such that A − LC has eigenvalues −1 and −2.
, such that A − LC has eigenvalues −1 and −2.
b: Let A, C, and L be the matrices from the previous part. Say that
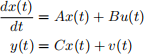
where v(t) is a measurement disturbance. If we have an observer of the form

and v(t) = 2 for t ≥ 0, calculate 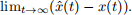
c: Consider a system of the form
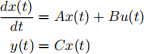
where A and C are given by
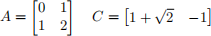
Explain why A−LC always has a positive eigenvalue for any gain vector, L. (Hint: Find a corresponding eigenvector.) Explain further, why this implies that an observer of the form
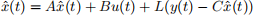
cannot be guaranteed to have 
2024-04-04