General

You must read fully and carefully the assignment specification and instructions.

Course: COMP20007 Design of Algorithms  @ Semester 1, 2024

Deadline Submission: Tuesday, 9th April 2024 @ 11:59 pm

Course Weight: 10%

· Assignment type: individual

ILOs covered: 2, 3, 4

· Submission method: via ED

Purpose

The purpose of this assignment is for you to:

· Design efficient algorithms in pseudocode.

· Improve your proficiency in C programming and your dexterity with dynamic memory allocation.

· Demonstrate understanding of a representing problems as graphs and implementing a set of algorithms.

Convex Hull

What is a convex hull?

A convex hull is a concept from geometry and computational geometry that refers to the smallest    convex set that contains a given set of points in a Euclidean space. Imagine you have a set of nails sticking out from a board; the convex hull is the shape you would get by stretching a rubber band around all the nails and letting it snap tight around them. The boundary created by the rubber band defines the convex hull.

More formally, a convex set is a set of points in which, for any two points within the set, the line

segment connecting them lies entirely within the set. The convex hull of a set of points is then the

smallest convex set that contains all those points. It is often visualized in two dimensions (2D) but can be extended to higher dimensions as well.

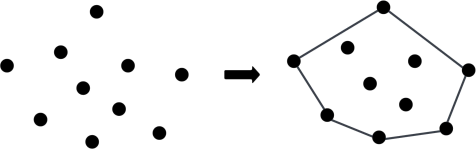
Computing the convex hull is a foundational problem in computational geometry because it is a

precursor to solving many other problems, such as finding the closest pair of points, and solving

various optimization problems. Several algorithms exist for computing the convex hull, with their

efficiency depending on the specific dimensions and characteristics of the point set. Examples of such algorithms include Graham's scan and Jarvis's march (also known as the gift wrapping algorithm) among others.

Applications

Convex hulls have numerous real-world applications. Some of the typical applications include:

· Image Processing and Computer Vision: Convex hulls are used in image processing for

object detection, recognition, and segmentation. They help in identifying the outer boundary of objects and separating foreground objects from the background.

· Geographic Information Systems (GIS): In GIS, convex hulls are utilized for spatial analysis, such as identifying the boundary of a geographic region or finding the convex hull of a set of   spatial data points.

· Robotics and Path Planning: Convex hulls play a vital role in robotics for path planning,  obstacle avoidance, and navigation. They help robots efficiently navigate through complex environments by identifying obstacles and determining safe paths.

· Collision Detection in Physics Simulations: In physics simulations and video games, convex hulls are used for collision detection between objects. They help determine if two objects

intersect or collide with each other.

· Pattern Recognition: Convex hulls are employed in pattern recognition tasks, such as hand- written character recognition, signature verification, and fingerprint matching. They aid in

extracting important features and reducing the dimensionality of data.

Convex Hull Computation Algorithms

Jarvis March

Initialization:

Start by selecting the leftmost point among the given points as the starting point of the convex hull. If there are multiple leftmost points, choose the one with the lowest y-

coordinate.

Add this point to the convex hull.

March:

Iterate through all the points to find the next point on the convex hull.

To find the next point, start from the current point and choose the point that has the largest counterclockwise angle with respect to the current point.

This is done by comparing the slopes of the line segments formed by the current point and each of the other points.

The point with the largest counterclockwise angle is the next point on the convex hull.

Add this next point to the convex hull.

Termination:

Repeat the main loop until the next point on the convex hull is the same as the starting point.

Once the next point becomes the starting point, the algorithm terminates.

Output:

The output of the algorithm is the list of points that form the convex hull, ordered in counterclockwise order.

The time complexity of the Jarvis March algorithm is O(nh), where n is the number of input points and his the number of points on the convex hull. In the worst case, where all points are on the convex hull, the time complexity is O(n2 ).

Pseudocode

JarvisMarch(points):

//  Ensure  there  are  at  least  3  points

if  length(points)  < 3:

return  empty  convex  hull

//  Initialize  an  empty  list  to  store  convex  hull  points

convexHull  <- empty list

//  Find  the  leftmost  point  (pivot)  among  the  given  points

leftmost  <- leftmost_point(points)

//  Start  from  the  leftmost  point

current  <- leftmost

repeat:

//  Add  current  point  to  the  convex  hull

add  current  to  convexHull

//  Find  the  next  point  'nextPoint'   such  that  it  forms  a  counterclockwise  turn //  with  the  current  point  and  any  other  point  in  the  set

nextPoint  <- points[0]

for  each  point  in  points:

if  nextPoint  =  current  or  orientation(nextPoint,  current,  point)  =  counterclockwise: nextPoint  <- point

//  Set  'nextPoint'   as  the  current  point  for  the  next  iteration

current  <- nextPoint

//  Repeat  until  we  return  to  the  starting  point  (leftmost)

until  current  =  leftmost

//  Return  the  list  of  points  in  the  convex  hull

return  convexHull

Notes

leftmost_point(points) returns the point with the lowest x-coordinate (or the bottom-most point satisfying this condition in case of ties).

· orientation(p,  q, r) is a function that determines the orientation of three points. It returns:

0 if the points are collinear.

1 if they form a clockwise turn.

2 if they form a counterclockwise turn.

Example

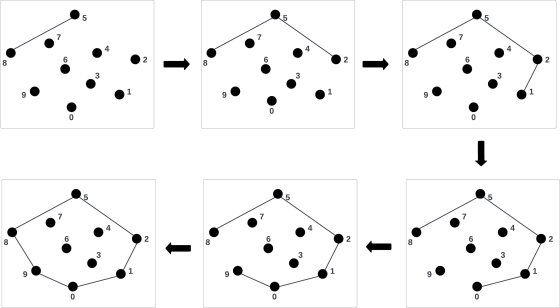
In the above example, the starting point is identified as point 8. We examine each point in relation to  point 8, determining which one results in the greatest counterclockwise turn compared to the rest. To put it more straightforwardly, the goal is to locate a point that ensures the line segment from the previous to the current point remains on the left side, while all other points are positioned to the right. As observed, point 5 is the initial choice because the line segment from point 8 to point 5 generates the most significant counterclockwise angle in comparison to the others. Following this logic, when positioned at point 5, we evaluate all other points and select point 2 as the one that yields the most pronounced counterclockwise turn. The process continues in this manner until it returns to   the starting point, which is point 8.

Graham's scan

Initialization:

Start by selecting the point with the lowest y-coordinate (or the leftmost point in case of ties) as the pivot point.

Sort the remaining points based on their polar angles with respect to the pivot point. If two points have the same polar angle, the one closer to the pivot point should come fi rst.

Scan:

Iterate through the sorted points and add them to the convex hull one by one.

For each point, check if it forms a counterclockwise turn with the two previously added points on the convex hull.

If it forms a counterclockwise turn, add the point to the convex hull. Otherwise, remove the last point from the convex hull until a counterclockwise turn is formed.

Repeat this process until all points are scanned.

Termination:

Once all points are scanned, the convex hull is complete.

Output:

The output of the algorithm is the list of points that form the convex hull, ordered in counterclockwise order.

The time complexity of Graham's scan algorithm is O(nlog n), where n is the number of input points. This complexity arises from the sorting step required to order the points based on their polar angles. The scanning step, where each point is checked and added to the convex hull, takes linear time.

GrahamScan(points):

//  Ensure  there  are  at  least  3  points

if  length(points)  < 3:

return  empty  convex  hull

//  Find  the  point  with  the  lowest  y-coordinate

lowest  =  point  with  lowest  y-coordinate  in  points

//  Sort  the  points  based  on  their  polar  angles  with  respect  to  the  lowest  point sort  points  by  polar  angle  with  respect  to  lowest

//  Initialize  an  empty  stack  to  store  convex  hull  points

stack  =  empty  stack

//  Push  the  first  three  points  to  the  stack

push  points[0]  to  stack

push  points[1]  to  stack

push  points[2]  to  stack

//  Iterate  over  the  remaining  points

for  i  =  3  to  length(points):

//  While  the  current  point  and  the  two  points  below  the  top  of  the  stack //  make  a  non-left  turn,  pop  the  top  of  the  stack

while  orientation(second_top(stack),  top(stack),  points[i])  !=  counterclockwise: pop  top  of  stack

//  Push  the  current  point  to  the  stack

push  points[i]  to  stack

//  The  stack  now  contains  the  convex  hull  points

return  stack

Notes

· lowest represents the point with the lowest y-coordinate in the set of points.

· sort  points by  polar angle  with respect to lowest sorts the points based on their polar angles with respect to the lowest point. If two points have the same polar angle, the one closer  to the lowest point comes fi rst.

· second_top(stack) returns the second topmost point in the stack.

orientation(p,  q,  r) is a function that determines the orientation of three points. It returns:

0 if the points are collinear.

1 if they form a clockwise turn.

2 if they form a counterclockwise turn.

Example

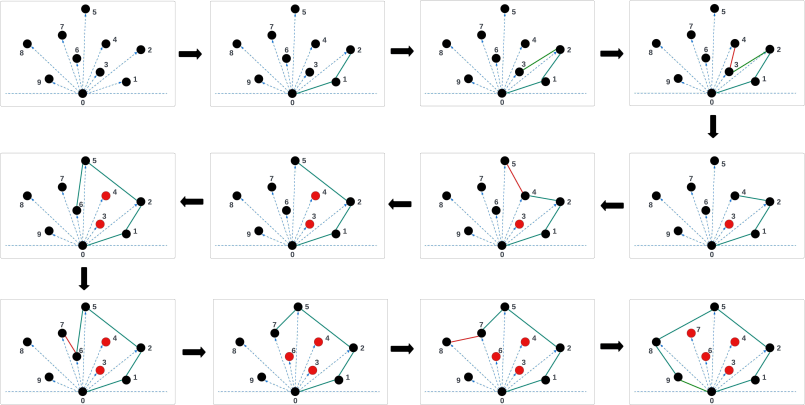
In the above example, point 0 is identified as the point with the lowest y-coordinate. Subsequently,    the other points are arranged based on their polar angles relative to point 0. Initially, points 0, 1, and 2 are placed into the stack. The addition of point 3 to the stack occurs because it facilitates a left turn in relation to the preceding two points (points 2 and 1). Conversely, point 4 induces a right turn compared to the last two points in the stack (points 3 and 2), leading to the removal of point 3 from  the stack. This adjustment allows for a left turn when point 4 is added atop point 2 in the stack. The  algorithm continues in this manner, examining each point in turn. Upon completion, the stack holds all points forming the convex hull.

Task 1: Convex Hull Computation with Doubly Linked Lists

Part A

Implement the Jarvis' March algorithm to compute the convex hull. Find the leftmost point. Then iterate over the remaining points, selecting the most counterclockwise point relative to the current point until you come back to the starting point.

Requirements

· Data Structure: Implement a doubly linked list to store the points of the convex hull. Each node should store the x andy coordinates of a point and pointers to the next and previous  nodes.

Input Format: The input will be a CSV file where the first line indicates the total number of points. Subsequent lines represent points with their x andy coordinates separated by a space (e.g.,  x  y ).

· Output Format: Your program should output two sequences of points forming the convex hull: one in clockwise order and the other in counterclockwise order. This should be done by  traversing your doubly linked list to print the points in both clockwise and counterclockwise   order, in both cases starting from the first point added to the hull. This may require starting    from a specific point and moving in one direction for clockwise and the opposite direction for counterclockwise. This should be output to the console (stdout).

Part B

Implement the Graham's Scan algorithm to compute the convex hull. Find the bottom-most point,   sort the points, and proceed with the scan, pushing and popping points from the stack (which will be your doubly linked list in this case) to ensure you maintain a convex hull throughout.

Requirements

· Data Structure: Implement a stack with doubly linked lists. Utilize this stack in Graham's Scan algorithm to store the convex hull points. Each node should store the x andy coordinates of a   point and pointers to the next and previous nodes.

· Input Format: The input will be a CSV file where the first line indicates the total number of    points. Subsequent lines represent points with their x andy coordinates separated by a space (e.g.,  x  y ).

· Output Format: Your program should output two sequences of points forming the convex  hull: one in clockwise order and the other in counterclockwise order. This should be done by traversing your doubly linked list to print the points in both clockwise and counterclockwise  order, in both cases starting from the first point added to the hull. This may require starting from a speciic point and moving in one direction for clockwise and the opposite direction for counterclockwise. This should be output to the console (stdout).

Part C

Evaluate both algorithms through experimental analysis by quantifying the total basic operations across various input scales and conigurations. Consider creating input sets of at least three distinct sizes, each under three difering distribution conditions: random, points on a circle, and random points contained within a set of points making up a simple hull.

You should use the following basic operations for each algorithm:

Jarvis' March - A comparison between the angles of points.

· Graham's Scan - A comparison between the angles of points during the sort.

Reporting: Write a report including a discussion on the choice of data structure, the experimental

evaluation, and conclusions drawn from the comparisons. Include any assumptions or simpliications made in your implementations.

Submission Guidelines

· Submit your C source code iles with appropriate comments explaining the algorithms and data structures used.

Your report should be in PDF format, including your indings from the experimental evaluation and any observations regarding the performance of the two algorithms.

Grading Criteria

· Correctness of the implemented algorithms and adherence to the requirements. · Efficiency and proper use of the doubly linked list for storing the convex hull.

· Clarity of the report, including the depth of the experimental evaluation and the analysis of the results.

· Code readability, structure, and documentation.

Task 1: Assignment Submission

Upload your solution to Task 1!

Input Formats

The test cases for each problem are present in the  test_cases  folder, and the expected answers for each of these test cases are present in the test_case_answers  folder.

Part A

The input for 1A is the number of points, followed by each point.

Example

3  (Number  of  points  we  are  constructing  the  hull  for)

0  0  (Point  1)

5  6  (Point  2)

2  3  (Point  3)

Part B

The input for Part B is the same as Part A.

Part C

Add your answers to Part C as a pdf called  written-tasks.pdf . Submit your assignment using the "Mark" button. You may submit as many times as you like.

Task 2: Baldur's Door

Baldur's Door is a new computer role-playing game based on the setting of a popular table-top game called Delves & Drakes, the game features an extensive variety puzzles and mechanics which critics have lauded as interesting and allowing for diverse modes of play. The game's characters take on quests which lead to puzzles.

Part A

In the early quests of the game, the town's tavern is advertising exciting new flavours for their soups. The cook has promised 500 silver pieces for each novel ingredient on their list gathered. Though

appearing generous for ingredient gathering in the nearby forest, the party cleric noticed that each    ingredient requires crawling between poison bushes. The party rogue has the smallest build and will likely be able to crawl through the bush without being scratched too badly - but will surely be afflicted. Once the poison takes hold, each step taken will passively do a ixed amount of damage.

The cleric's healing spell can only be casted once the party rogue has exited the narrow space. Since each casting of the healing spell requires expensive magical materials, you will have to ind the route that reaches the exit in the least possible steps.

An example of the forest pathways are shown below, where each edge represents a step and each node represents a location the rogue can step to:

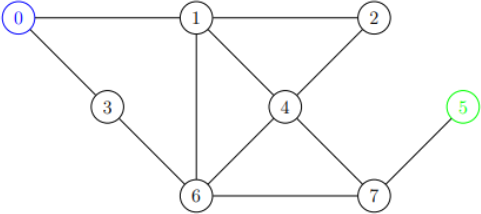
The forest layout above would be represented by the input to your program:

8

11

0

5

0  1

0  3

1  2

1  4

1  6

2  4

3  6

4  6

4  7

5  7

6  7

Where:

the first line ( 8 ) is the number of locations the rogue can possibly step,

the following line ( 11 ) is the number of connections between locations,

the third line ( 0 ) is the location the rogue starts at,

the fourth line ( 5 ) is the location the rogue exits the space and is in range to be healed, and all following lines are pairs, indicating an undirected connection between the two locations.

You may assume the list is sorted numerically by the first location and then (where the first location is equal) by the second location. You may also assume locations are always equal to or greater than 0 and numbered less than the number of locations.

The output should be the damage taken - assuming one point of damage is taken per step.

Part B

After hearing the ease with which our protagonists were able to deal with the poison forest, a local merchant staying at the tavern asks if the party would be interested in a challenge. The merchant had come into possession of a number of lair maps that showed the locations of all the traps in each lair. The merchant confessed they did not have any non-mercantile skills but had managed to purchase information on how to disarm each trap. After discussing the skills the party held, the merchant explained the cost of the materials they'd need to disarm each trap they had the skills to disarm and marked this total cost on each pathway. To preserve the most treasure, you'll need to find the cheapest path through the lair.

Here is an example of one of these maps:

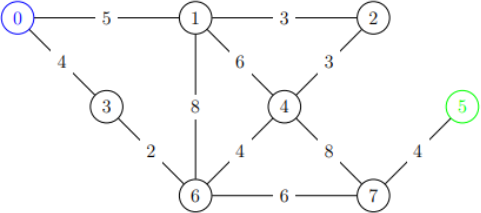
This map would be represented using the following format:

8

11

0

5

0  1  5

0  3  4

1  2  3

1  4  6

1  6  8

2  4  3

3  6  2

4  6  4

4  7  8

5  7  4

6  7  6

Which is the same as the format for Part A, but each edge specified includes an additional third number describing the cost of disarming the trap. You may also assume that all costs will be non- negative.

Part C

To reward the adventurers for their extensive help connecting the merchant with their extensive treasures, they share their own prior connections. The documents they share detail artisans who will ofer ongoing services for a particular price - each artisan on the map is able to create one material   from another and reverse the process. Each document is limited to the connections for a particular set of materials which are related in some way. Since the general store merchants ofer a new daily special periodically, having a network which allows the creation of all materials from any material in the documents will save a lot of money in future adventures. You will have to find the gold you'll need to build the network which allows any material to be reached from any other material in the document.

Here is an example of one of these documents:

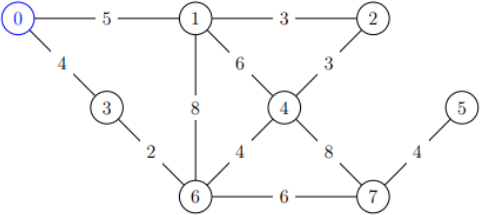
This document would be represented using the following format:

8

11

0

0  1  5

0  3  4

1  2  3

1  4  6

1  6  8

2  4  3

3  6  2

4  6  4

4  7  8

5  7  4

6  7  6

Which is similar to the format for Part B, but excludes the fourth line that would normally specify the final destination.

The output will be the minimum cost required to pay across all artisans such that each material in the document can be made from any other material.

Part D

The final battle with Balgor, the Ruler of the Delve requires venturing into the eponymous mythic delves. Mythic delves are typically reserved for the strongest of adventurers, as each room applies a further unique condition which increases the amount of damage done. Those who came before you   have managed to map the damage multiplier that each room applies, and have sold these precious    maps to you for a hefty sum. Since one of Balgor's minions lies at the end of each mythic delve, you  will have to reach the end of the delve with the lowest multiplier to have any chance of besting them.

The game uses the mathematical floor of the calculated multiplier when calculating the final damage multiplier (as this multiplier is displayed to the player as a whole number) - however this is only applied to the final value, intermediate calculations retain the fractional elements.

Here is an example of a map of a mythic delve:

This map would be given in the following format:

8

10

0

7

0  1  20

0  2  30

1  2  10

2  3  60

3  4  80

3  6  20

4  5  20

5  6  10

5  7  90

6  7  120

This is similar to the format of Part A and B, but the weight of each edge is the percentage increase (e.g. a value of 20 implies a 20% increase in the damage taken in each subsequent room). For this   problem, successive rooms multiply by the weight of the previous rooms, so in the above map, a   path which takes the edge between 0 and 1, followed by the edge between 1 and 2, would apply a total increase of 32%.

The output should be the final percentage increase (without the percent sign) with any fractional part of the percentage omitted.