Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

EECS 203: Discrete Mathematics

Fall 2021

Homework 8

This homework should be submitted as a PDF through Gradescope (see instructions on course site for more details). We strongly prefer students to compose homework solutions using a word processor (Google Docs or MS Word), or ideally using LATEX, but we will accept handwritten homework submissions scanned/photographed and converted to PDF. Note that submitted files must be less than 50 mb in size, but they really should be much smaller than this. No email or Piazza regrade requests will be accepted. For more detail on regrade requests, please refer to course policies.

● We will not grade homework problems that were not properly matched on Gradescope. Please submit early and often and double-check that you matched your pages to their question.

● Explanation or justification for yes/no, true/false, multiple choice questions, and the like: You must provide some sort of explanation or justification for these types of questions (so we know you didn’t just guess), unless explicitly specified below. For example, simply answering “true” for a T/F question without providing an explanation will receive little or no credit.

● All problems require work to be shown. Questions that require a numerical answer will not be given credit if no work/explanation is shown.

● Honor Code: By submitting this homework, you agree that you are in compliance with the Engineering Honor Code and the Course Policies for 203, and that you are submitting your own work.

● Hyperlinks on Submitting Homework to Gradescope: Instructions or Youtube Video

Individual Portion

1. Classes in Class [2 points]

Assume there are four IAs who are working in a group together: Daniel, Forest, Matt, and Rafael. Suppose we have a relation R on this group of IAs, and (a, b) ∈ R if and only if a has a name beginning with a letter in the same half of the alphabet as b (Note: the alphabet can be split in half from A to M and from N to Z).

a) Show that R is an equivalence relation.

b) List all the equivalence classes of R.

2. Equivalence Relations [3 points]

Suppose that R1 and R2 are equivalence relations on the set S. Determine whether each of theses combinations of R1 and R2 must be an equivalence relation.

a) R1 ∪ R2

b) R1 ∩ R2

c) R1 ⊕ R2

3. David HasseHoff [3 points]

Consider the set S = {1, 2, 3, 4, 5, 6, 7, 8} and the following partial order:

R = {(2, 5),(7, 6),(7, 5),(3, 6),(4, 6),(5, 6),(1, 6),(4, 1),(2, 6),

(1, 1),(2, 2),(3, 3),(4, 4),(5, 5),(6, 6),(7, 7),(8, 8)}

(a) Construct the Hasse diagram for (S, R).

(b) Determine if it has any maximal, minimal, minimum, or maximum elements and if it does, give such elements.

(c) Find two compatible total orderings of R.

4. To the Max [2 points]

Let P be a nonempty poset. For each of the following, explain in one or two non-rigorous sentences why the statement is true or provide a valid counterexample:

a.) P must contain a maximum element.

b.) P must contain a maximal element.

c.) If P is finite, P must contain a maximum element.

d.) If P is finite, P must contain a maximal element.

Remark: After completing this problem, you may conclude the analogous statements you proved/disproved above about minimum and minimal elements.

5. Graphs and Networks [2 points]

Explain how graphs can be used to model email messages in a network. Make sure your answer addresses each of the following (with brief justification for ii-iv):

(i) what the edges/vertices represent

(ii) if edges should be directed or undirected

(iii) if multiple edges should be allowed

(iv) if loops should be allowed

6. Degree-sy Peasy Lemon Squeezy [1 point]

a) A given undirected graph has 6 edges in total. Find the sum of the degree of each vertex in the graph.

b) For a given directed graph, the list of the in-degree of each vertex is 3, 2, 4, 0, 1, 1. Find the number of edges in the graph.

7. Edgy Graphitti [1.5 points]

K4 is a complete graph with 4 vertices, and C7 is a cycle with 7 vertices. Suppose these share 3 vertices. How many distinct edges will there be in K4 ∪ C7 assuming the shared vertices are

a) 3 Consecutive in the cycle

b) 2 Consecutive and 1 other

c) No two vertices are consecutive

8. Vertices and Edges [2 points]

Can a simple graph have 6 vertices and 16 edges? If so, draw it, if not, explain why not.

Group Portion

Grade Groupwork 7

Using the solutions and Grading Guidelines, assess your Groupwork 7:

● Construct a table to assess your previous week’s work, below is an example of such a table.

● Please include your original groupwork submission in this grading submission, marking up the original submission for revisions

● For each rubric item, indicate whether or not your/your group’s submission achieved this rubric item.

● For rubric items that weren’t achieved, please visually indicate, whether with a sen-tence, annotation, mark-up, correction, or similar why your submission did not receive this item.

● You do not have to “redo” the problem correctly for the grading portion, however this is recommended.

● If your group submitted the same groupwork for the previous week, you may grade the same thing together. If not, we want you to give a grade of your version. Again, you could discuss this together or on your own.

● For extra credit, write yourself positive remark(s) associated to your work.

1. Less Than and Equal To [4 points]

Let S = {1, 2, . . . , n} and let R be a relation on S that is both an equivalence relation and a partial order.

(a) What is the matrix of R?

(b) If n > 1, what are the minimal/maximal elements, are there any maximum elements?

(c) Describe or Draw the Hasse diagram of (S, R).

(d) What are the equivalence classes of (S, R)?

(e) For n > 1 Give two distinct compatible total orders of (S, R)

(f) For which n ∈ Z⁺ is (S, R) a total order

(g) If n > 1 What is GLB{1, 2}? What is LUB{1}?

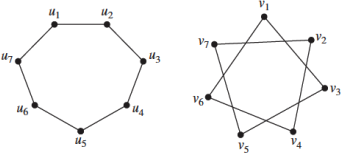
2. Isomorphism Intro [5 points]

Consider the two graphs shown below.

(a) First, let’s compare these graphs. How many vertices do each of the graphs have? How many edges? Compare these numbers. Then, for each of the graphs, list the degrees of each of the vertices. How do these lists compare?

(b) Next, we will use these comparisons to look for a one-to-one correspondence (bijection) between the vertices of the two graphs. Such a correspondence would create identical paths between vertices. This means that, for every edge connecting two vertices of one graph, there must be an edge connecting their corresponding vertices in the other graph. If a bijection exists, list the corresponding vertices. If not, explain briefly why not.

(c) Finally, analyze whether such a bijeciton is unique. If a bijection exists between two graphs, could there be other bijections that are different, but also valid? If you found a bijection in part (c), then either: (i) give a different bijection, and the total number of different possible bijections between the vertices of these particular graphs, or (ii) explain why your bijection is unique for this example. If you did not find a bijection in part (c), then draw your own simple example of two graphs whose vertices have a bijection, and count the number of different bijections that exist in that example.

Note: Two graphs that maintain such a correspondence are called Isomorphic.