EE 4233 - Spring 2022 Exam 2
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
EE 4233 - Spring 2022
Exam 2
This exam has 3 questions each with 3 parts. Each part is worth 10 points. Show all your work.
Answers without work or explanation may lose credit.
Problem 1: Bounded-Input Bounded-Output (BIBO) Stability
a: Determine if the following system is BIBO stable
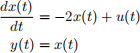
b: Determine if the following system is BIBO stable

c: Consider a system of the form:

where A11, A22, A33, and A44 are square matrices. In order for this system to be BIBO stable, only one of the matrices A11, A22, A33, and A44 is required to have negative real-part eigenvalues. Explain why this is true, and determine which of the matrices must have negative real-part eigenvalues.
Problem 2: Asymptotic Limits of Signals
a: Say that
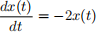
and x(0) = 1. What is limt→∞ x(t)?
b: Say that
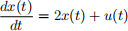
with x(0) = 0 and u(t) = 1 for t ≥ 0. (i.e. u(t) is the unit step). Calculate limt→∞ x(t) and lims→0 sX(s). Briefly why the final value theorem does apply in this scenario.
c: Let  , where x1(t) and x2(t) are vectors. Say that
, where x1(t) and x2(t) are vectors. Say that

where A22 is a square matrix whose eigenvalues have negative real parts. Explain why that limt→∞ x(t) exists and compute limt→∞ x(t).
Hint: To show that limt→∞ x(t) exists, you can get an expression for x(t) in terms of the initial condition, x(0).
Problem 3: Stabilizability and Detectability
a: Say that
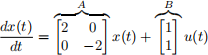
Find a gain, K, such that the eigenvalues of A − BK have negative real parts.
b: Say that
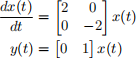
Find an initial condition, x(0), such that limt→∞ x(t) = 0 and y(t) = 0 for all t ≥ 0.
c: Consider an interconnected system of the form

Assume that the system 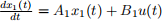 is stabilizable and is stabilizable and the matrix A2 has negative real-part eigenvalues. Explain why the system with state
is stabilizable and is stabilizable and the matrix A2 has negative real-part eigenvalues. Explain why the system with state  is also stabilizable.
is also stabilizable.
2024-04-03