PHL349 TAKE-HOME EXAM
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
PHL349 TAKE-HOME EXAM
Each of the problems below is worth 12.5 points.
1. Prove the statement that every countably infinite partially ordered set <A, R> is isomorphic to one of its proper subsets <B, R↾B> or provide a counterexample to it.
2. Prove the statement that any partial ordering can be extended to a linear ordering [i.e. that if <A, R> is an arbitrary poset then there exists S  A2
such that R
A2
such that R  S and <A, S> is a linear ordering] or provide a counterexample to it.
S and <A, S> is a linear ordering] or provide a counterexample to it.
3. Prove the well-ordering theorem from Zorn’s lemma without appealing to other forms of the axiom of choice [Hint: see exercises 21 and 22 in Chapter 7 of Enderton’s book].
5. Let  and let Pt(A) be the set of all partitions of A [see p. 57 in Enderton’s book]. Define a relation ≼ on Pt(A) by
and let Pt(A) be the set of all partitions of A [see p. 57 in Enderton’s book]. Define a relation ≼ on Pt(A) by
S1 ≼ S2 if and only if for every C in S1 there exists D in S2 such that C  D.
D.
a) Show that ≼ is an order relation.
b) Show that if U  Pt(A) then U has both an infimum and a supremum [see p. 171 in Enderton’s book for definitions of these notions].
Pt(A) then U has both an infimum and a supremum [see p. 171 in Enderton’s book for definitions of these notions].
6. Define a permutation of K to be any one-to-one function from K onto K. If K = cardK, then K! is card{f | f is a permutation of K}. Show that if K is infinite, then

7. Let ℵ1 be the smallest uncountable ordinal [see p. 199 in Enderton’s book]. Show that

without using the axiom of choice.
8. a) Show that if β < λ, λ a limit ordinal, then  b) Show that if β < λ, λ a limit ordinal, then
b) Show that if β < λ, λ a limit ordinal, then  c) Show that if
c) Show that if 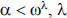 a limit ordinal, then
a limit ordinal, then  d) Show that
d) Show that  cannot be written as
cannot be written as  where
where 
2024-04-02