Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

1.  (30 points)  The goal of the problem is to show that the dimension of the column space of the matrix is equal to the dimension of the row space of the matrix.

(a)  (5 points)  Define elementary column operation over the matrices as following  (i) Pick a column with entries v, replace other column w as αv+w for some α ∈ F; (ii) Switch the location of two columns.  Show that the column space remains invariant after any elementary column operation.

(b)  (5 points)  Define elementary row operation analogously.  Let a1 ,..., an  be the orig-

inal column, and a1(′),..., an(′)  be the columns after applying an elementary row oper-ation. Show that 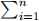： αiai  = 0 iff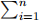： αi ai(′) = 0

(c)  (10 points)  Prove Gaussian Elimination.  That is there exists a sequence of elemen- tary row/column operations which transforms any given matrix M ∈ Fm ×n  into the block form of（ C(A)   D(B)) where the entries of B, C and D are all zero (they could be empty) and A is diagonal (only non-zero entries are on the diagonal)

(d)  (10 points)  Using the previous statements, conclude that both the dimension of the column space of the matrix and the dimension of the row space of the matrix remains invariant under elementary row and column operations, and that they are equal.

2.  (10 points)  Prove Cauchy-Schwarz Inequality, that is

3.  (10 points)  Use  Steinitz Exchange  Principle to show that the notion of dimension is well-defined. That is for any given two basis B1  and B2  of a vector space V ,  |B1 | = |B2 | .