In this unit, we are looking at Alan Turing’s formalization of “computable functions” using Turing machines. I have posted Turing’s famous paper On Computable Numbers (Turing, 1937a) on BlackBoard for you.

The lambda (λ) calculus is an alternative formulation of computable functions developed by the mathematician Alonzo Church around the same time that Turing was developing his machine model (Church, 1936).  The two formalizations have been proven equiva- lent, in that any function computable using one of them can be computed using the other. Turing actually discussed this in an appendix to his famous paper, and in a subsequent paper (Turing, 1937b). The Church-Turing thesis states that these and other equivalent formalisms completely define the informal notion of an “algorithm” or computable func- tion.  So far no alternative model has been proposed that can compute anything that can’t be done with either Turing machines or the lambda calculus.

Functional programming is based on the lambda calculus (at least in part). In this project, we will take a short break from C and do a bit of functional programming.  However just like actually programming a Turing machine is quite involved, programming directly using the lambda calculus would be painful.  Very, very painful.  So instead, this term we will use the original functional programming language: Lisp.

If you are new to Lisp, and most students will be, please check out the accompanying “Notes on Lisp for CSC173” that I have posted with this project description.  It will take some time for you to get comfortable programming in Lisp. Be prepared to go to a study session if it is new to you.

You should probably bookmark the Common Lisp HyperSpec, which documents all of Common Lisp (but is a reference, not a tutorial).  However see Project Requirements, below, regarding which builtin features of Common Lisp you may use in this project.

In mathematical notation, we might write that as follows:

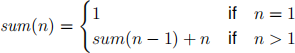
In a functional programming language, the program will look just like the definition! Per- haps something like this:

def  sum(n):

n  =  1:  1

n  >  1:  sum(n-1)  +  n

Note that there is no “return” statement here. We’re not telling the computer what to do. If n is 1, the sum is 1. That’s what it says.  If n > 1, the sum is something else and we’re given an expression for computing it.

Of course, you could also write the Java method recursively:

int  sum(int  n)  {

if   (n  ==  1)  return  1;

if   (n  >  1)  return  sum(n-1)  +  n;

}

BTW: If you actually try this code, your Java compiler should complain.  But you could fix it up.

The key to functional programming is to think declaratively (“say what something is not how to compute it”). Very often that will involve recursion. What is a recursive definition of a list of, say, numbers? What is a recursive definition of the sum of a list of numbers? What does it mean to “filter” a list of numbers recursively to keep or remove some of them? That’s how you need to think in order to program functionally.

All (almost all?) functional programming languages support some aspects of imperative progranmming.  In fact, it is possible to write almost purely imperative programs using Lisp (or most practical functional programming languages). But that is not the goal for this project. Your code should be as purely functional as possible. For that reason, you are only allowed to use a subset of Lisp features, as described below. 

Here’s what Paul Graham, the founder of legendary tech incubator Y Combinator, has to say about learning to program in Lisp:

For alumni of other languages, beginning to use Lisp may be like stepping onto a skating rink for the first time.  It’s actually much easier to get around on ice than it is on dry land—if you use skates.  Till then you will be left wondering what people see in this sport.

What skates are to ice, functional programming is to Lisp.  Together the two allow you to travel more gracefully, with less effort. But if you are accustomed to another mode of travel, this may not be your experience at first. One of the obstacles to learning Lisp as a second language is learning to program in a functional style. (Graham, 1994, p. 33)

Graham goes on to describe a way of making this mental shift.  I’ve posted a longer

excerpt from his book On Lisp on BlackBoard with the readings for this unit.

Our textbook also discusses this:

There is a common belief that it is easier to learn to program iteratively, or to use nonrecursive function calls, than it is to learn to program recursively. While we cannot argue conclusively against that point of view, we do be- lieve that recursive programming is easy once one has had the opportunity to practice the style.  Recursive programs are often more succinct or easier to understand than their imperative counterparts. More importantly, some problems are more easily attacked by recursive programs than by iterative programs [for example, searching trees]. (Aho and Ullman, 1995, pp. 69–70)

Project Requirements

You must implement the four functions from each of the “List,” “Set,” and “Math” sections below. So twelve (12) functions total. Don’t worry—most of them can be done in no more than a few lines of Lisp.

In some cases, these functions are already defined in Lisp.  We could simply let your definitions replace the builtin ones.  But to ensure that we are testing your functions, all the functions that you must write have names that start with a period (or dot, “ . ”). Your functions must use the correct names so that we can test them.  Of course you may also define helper functions, or reuse functions that you have written yourself to implement another required function.

NOTE: You may use only the following builtin features from Common Lisp:

•  Constants: t, nil, numbers

• Quotation: quote or “ ’”

• Type functions: listp, consp, numberp, atom (no “p”),etc.

•  List functions: cons, car, cdr, list, null

•  Function functions (!):  defun, funcall, apply, lambda (not really a function but. . . )

•  Equality functions: eq, eql, =, equal, equalp

•  Math operators:  + (addition),  - (subtraction), * (multiplication), / (division); you may not use the built-in modulus (mod) or remainder (rem) functions, but they have straightforward recursive definitions so you can easily write your own if you need them

•  Comparison operators: >, >=, <, <=

•  Boolean operators: and, or, not (you could easily write these yourself)

•  Conditional functions: cond, if, when, unless (you could easily write all of these using cond)

Note that you may NOT use imperative programming forms like let,  setq, progn, loop, or return in the definitions of your functions.  Be functional. You might also find the freely-available book How to Design Programs helpful.

Your submission must be a single Lisp ( .lisp) file, in addition to your README or other documentation. We will load your file into Lisp and then test the required functions on a range of inputs. You will get points for the functions that are correct.

There is no opportunity for extra credit on this project.

Note on functions that take other functions as arguments

For functions that take another function or functions as parameter(s), you will need to use apply or funcall to invoke the given function.

For example:

(defun  twice   (f  x)

"Returns  the  result  of  applying  function  F  twice  to  argument  X . " (funcall  f   (funcall  f  x)))

(twice   'sqrt  16)  ;  =>  2.0

(twice   '1+  7)  ;  =>  9

(twice   'cdr   '(a  b  c  d))  ;  =>   (C  D)

(twice  'car   '((a  b  c)   '(d  e  f)))  ;  =>  A

The difference between funcall and apply is that funcall takes a function as its first argument and passes any remaining arguments to the function, while apply takes a function and a list as its two arguments, and “applies” the function to the list of argu- ments, meaning that that the elements of the list become the arguments to the function.

List Functions

You may assume that any arguments to these functions that are supposed to be lists are in fact lists. That is, you do not need to check that they are lists (using listp, for example).

(.element-of  X  L):  Returns true (non-nil) if the element X is an element of the list L (test elements with equalp),otherwise false (nil)

(.element-of  3   '(1  3  x  a))  =>  T

(.element-of  2   '(1  3  x  a))  =>  NIL

(.reverse  L):  Returns a list that contains the same elements as the list L, but in the reverse (opposite) order

(.reverse   '(a  b  c  d))  =>   (d  c  b  a)

(.reverse   '())  =>  NIL

(.sum  L):  Assuming that list L contains numbers, returns their sum

(.sum   '(1  2  3  4))  =>  10

(.sum  nil)  =>  0

(.filter  F  L):  Returns a list containing only those elements of L for which Boolean function F returns true (non-nil)

(.filter   'numberp   '(1  a  3  "xyz"  5   (a  b  c)  nil))  =>   (1  3  5) (defun   .lessthan3   (x)   (<  x  3))

(.filter  '.lessthan3   '(1  4  5  2  1  6))  =>   (1  2  1) (defun   .lessthany   (y)   (lambda   (x)   (<  x  y))

(.filter   (.lessthany  3)  '(1  4  5  2  1  6))  =>   (1  2  1)

Set Functions

Set functions use lists to represent sets, but of course sets may not contain duplicate elements. You may assume that any sets (lists) given as arguments to these functions are lists that satisfy that requirement.  That is, you do not need to check that it is true for sets (lists) given as argument. But of course you do need to ensure that it is true for sets that are the result of any of your functions.

(cardinality  S):  Returns the cardinality of (number of elements in) set S

(.cardinality  '())  =>  0

(.cardinality  '(a  b  c))  =>  3

(.contains  S  X):  Returns true (non-nil) if the set S contains the element X (test elements with equalp),otherwise false (nil)

(.contains   '(b  c  a  d)   'a)  =>  T

(.contains   '(b  c  a  d)   'z)  =>  NIL

(.intersection  S1  S2):  Returns the set that is the intersection of sets S1 and S2 (that is: L1  ∩ L2 ); test elements with equalp

(.intersection  '(a  b  c)   '(a  c  d))  =>   (A  C)

(.intersection  '(a  b  c)   '(x  y  z))  =>  NIL

(.subseteq  S1  S1):  Returns true (non-nil) if S1 is a subset of or equal to set S2 (that is, if S1  己 S2 ), otherwise return false (nil); test elements with equalp

(.subseteq   '(a  b)   '(a  b  c  d))  =>  T

(.subseteq   '(a  b  c  d)   '(a  b  c  d))  =>  T

(.subseteq   '()   '(a  b  c  d))  =>  T

(.subseteq   '(a  b  x)   '(a  b  c  d))  =>  NIL

Math Functions

You may assume that any arguments to these functions that are supposed to be numbers of some kind are in fact numbers of that kind.  That is, you do not have to check that they are numbers (using numberp, for example).

(.complex=  C1  C2):  Returns true (non-nil) if the complex numbers C1 and C2 are equal. Two complex numbers ⟨r1 , i1 ⟩ and ⟨r2 , i2 ⟩ are equal iff r1  = r2  and i1  = i2 . You may assume that complex numbers are represented using lists containing two elements where the first element is the real component of the number and the second element is the imaginary part of the number. Test numbers using =.

(.complex=   '(1.0  0.0)   '(1.0  0.0))  =>  T

(.complex=   '(0.0  1.0)   '(0  1))  =>  T

(.complex=   '(+1  -1)   '(-1  +1))  =>  NIL

(.mod  X  Y):  Returns the remainder when positive integer X is divided by positive in- teger Y

(.mod  7  3)  =>  1

(.mod  8  4)  =>  0

(.dot-product  V1  2):  Returns the dot product of vectors V1 and V2. The dot prod- uct of two vectors v1  = ⟨v1,1 , v1,2 ,..., v1,n⟩ and v2  = ⟨v2,1 , v2,2 ,..., v2,n⟩ is

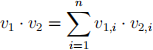
You may assume that vectors are represented as lists of their components.  You may also assume that V1 and V2 have the same non-zero number of components (the same length).

(.dot-product   '(1  2)   '(3  4))  =>  11

(.dot-product   '(1  2  3)   '(1  2  3))  =>  14

(.dot-product   '(9)   '(7))  =>  63

(.gcd  X  Y):  Returns the greatest common divisor  (GCD) of the two given  positive integers

(.gcd  8  12)  =>  4

Hint: Euclid could have written this function.

Project Submission

Your project submission MUST include the following:

1. A README.txt file or PDF document describing:

(a) Any collaborators (see below)

(b) Acknowledgements for anything you did not code yourself (you should avoid this, other than the code we’ve given you, which you don’t have to acknowl- edge)

(c) Any issues we should know about, limitations, or special things that you did.

2. All source code for your project in a single Lisp file

There is no submission form for this project.

Late Policy

Late projects will receive a grade of 0. You must submit what you have by the dead- line.  If there are extenuating circumstances, submit what you have before the deadline and then explain yourself via email.

If you have a medical excuse (see the course syllabus), submit what you have and explain yourself as soon as you are able.

Collaboration Policy

I assume that you are in this course to learn. You will learn the most if you do the projects yourself.

That said, collaboration on projects is permitted, subject to the following requirements:

• Teams of no more than 3 students, all currently taking CSC173.

• You must be able to explain anything you or your team submit, IN PERSON AT ANY TIME, at the instructor’s or TA’s discretion.

• One member of the team should submit code on the team’s behalf in addition to their writeup. Other team members must submit a README (only) indicating who their collaborators are.

• All members of a collaborative team will get the same grade on the project.

Working in a team only works if you actually do all parts of the project together.   If you only do one part of, say, three, then you only learn one third of the material.   If one member of a team doesn’t do their part or does it incorrectly (or dishonestly), all members pay the price.

Academic Honesty

I assume that you are in this course to learn. You will learn nothing if you do not do the projects yourself.

Do not copy code from other students or from the Internet.

Avoid Github and StackOverflow completely for the duration of this course.

The use of generative AI tools is NOT permitted in this course.

Posting homework and project solutions to public repositories on sites like GitHub is a vi- olation of the University’s Academic Honesty Policy, Section V.B.2 “Giving Unauthorized Aid.”  Honestly, no prospective employer wants to see your coursework.  Make a great project outside of class and share that instead to show off your chops.

Acknowledgements

Thanks to the always-functional Mikayla Konst for her contributions to this project back in the day.

References

Aho, A., and Ullman, J. (1995).  Foundations of Computer Science. W. H. Freeman and Company.