MAT 137Y: Calculus with proofs Assignment 8

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MAT 137Y: Calculus with proofs

Assignment 8

Due on Thursday, Apr 4 by 11:59pm via GradeScope

Instructions

This problem set is based on Unit 13 and 14.  Please read the Problem Set FAQ for details on submission policies, collaboration rules, and general instructions. Remember you can submit in pairs or individually.

. Submissions are only accepted byGradescope. Do not send anything by email. Late submissions are not accepted under any circumstance. Remember you can resubmit anytime before the deadline.

. Submit your polished solutions using only this template PDF. You will submit a single PDF with your full written solutions. If your solution is not written using this template PDF (scanned print or digital) then you will receive zero.  Do not submit rough work.  Organize your work neatly in the space provided.

. Show your work and justify your steps on every question, unless otherwise indicated.  Put your inal answer in the box provided, if necessary.

1. Write a power series with a radius of convergence of 1, converging on (2 ; 4) satisfying the following

extra conditions.  If no such power series exist, put “None” .  You don’t need to show the draft work about how do you get the series.

(a)  Conditionally convergent at x = 2 and x = 4.

(b) Absolutely convergent at x = 2, conditionally convergent at x = 4.

(c)  Conditionally convergent at x = 2, divergent at x = 4.

(d)  Divergent at x = 2, divergent at x = 4.

2. Let 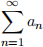be an ininite series.

Is each of these statements true or false?  If it is true, prove it.  If it is false, prove it by providing a counterexample and justify that is satisies the required conditions.

(a) If the  series  POSITIVE 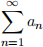is  convergent  (i.e.    an    >  0  for  all  n   ≥  1),  then  the  series 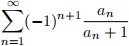is convergent.

True              False

(b) If the series 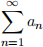is convergent, then 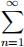arctan(an + n/1) is convergent.

True              False

(c) If the POSITIVE series 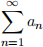is convergent and 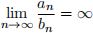with the sequence 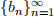is a POSITIVE sequence, then 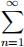ln(an + bn) is divergent.

True              False

(d) If the series 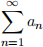is absolutely convergent and f is continuous on R, then 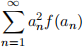is conver-gent.

True              False

3. Deinition: An Ininite Product 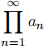= a1  · a2 · a3 · a4 · · · converges to L ≠ 0 2 R if the sequence of partial products 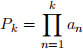converges to L. In other words, 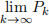Pk  = L.  If L = 0, then we say that the Ininite Product diverges to 0.

(a)  Prove that 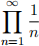diverges to 0 by using the deinition.

(b)  Prove that 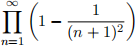converges to L for some L 2 R and L ≠ 0 by using the deinition. What is the L?

(c) We have two Theorems here:

Theorem A: Let {an}∞n=1 be a sequence where an ≥ 0 for any n ≥ 1. ∞n Y=1 (1 + an) converges if and only if the sequence of partial products Pk = kYn =1 (1 + an) is bounded.

Theorem B: Let {an}∞n=1 be a sequence. If ∞Xn=1 an converges then ∞ n Y =1 (1 + an) converges.

Mik thinks the theorem B is true, here is the proof of his argument:

1. From our assumption, say that 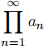= L

2. Take the ln of the partial products, ln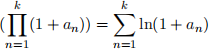

3. Now since 1 + x ≤ e x , it follows that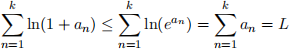

4. This means that 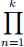(1 + an) is bounded so applying theorem A, we can conclude convergence.

Sarah disagrees, here is her counter example:

Let 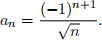Then the infinite series 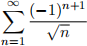converges by the alternating series test, but the infinite product 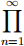(1 + an) diverges to 0.

(1) What assumption needs to be added to theorem B so that it is true?

(2) Why can we take the ln of the partial products? You answer should be one short sentence.

(3)  Prove the Theorem A.

Hint:  you may need to use the Monotone Convergence Theorem in your proof.

(4) In step 4 of Mik’s Proof, he concluded that 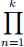(1 + an)  is bounded without showing the rigorous proof. Fix it.

(5) By adding the assumption in Theorem B, we can prove the modified version of Theorem B: “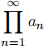 converges if and only if 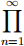(1 + an) converges.” One direction has been proved by Mik. You will prove another direction: if 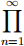(1 + an) converges then 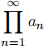converges.

(6)  Does the ininite product 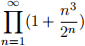converge? Justify your answer.

n=1

Hint: you may need to use the modiied Theorem B.

4. Approximations only hold value if you can estimate the error of your approximation.  Often only a certain error threshold is tolerable. This leads to a natural question:

What order of approximation N do I need to  estimate

my function at x with d digits  of accuracy?

The answer depends on the function f , the value x at which you want to approximate it, and the distance between x and the centre of your approximation.  It is helpful to express N in terms of a simple inequality involving d and x.

Let N 2 Z+. Let PN(x) be the N th Taylor polynomial of sin x centred at 0.

(a)  Deine RN(x) = sin x — PN(x) to be the N th remainder term.  Show that

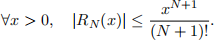
(b) Approximate sin 5 by inding the smallest N such that sin 5 ≈ PN(5) and the error within 10-2 .

(c) Now, you will generalize your approximation of sin x for any x > 0 with arbitrary accuracy.  To more simply estimate the quality of your error term, it helps to understand precisely how factorials grow. Stirling’s approximation says that

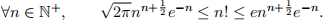
Use Stirling’s approximation to show that

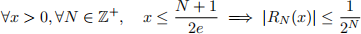
Hint:  Use (a) and the inequality for x to estimate |RN(x)| with an expression in terms of N only. Remember estimates do not need to be exact.  They just need to be good enough.  That is why they are called estimates.

(d) What order of approximation N can estimate sin x within 10-d?

Use (c) to give a simple inequality for N depending on x and d.




2024-03-29