1.  Pretense of democracy: You can see a brief description of (avariant of) this model here.

Consider a setting with two players: a dictator and an opposition. Both players have a common prior belief about the dictator’s popularity θ: with probability γ > 0, θ = 1 (the dictator is popular) and with the remaining probability 1 − γ , θ = 0 (the dictator is unpopular).  The dictator can call for an election which conveys information about his popularity. Specifically, the election takes the form of a signal v which takes the value 1 with probability 1 if θ = 1, and takes the value 1 with probability ϕ if θ = 0 where ϕ ∈ [0, 1] measures the extent to which the dictator can interfere in the election. ϕ is chosen by the dictator at the start of the game and is costless for the dictator.

The opposition observes ϕ and the outcome of the election (that is, v = 0 or v = 1) and decides whether to challenge the dictator at a cost of η ∈ (0, 1). A challenge is successful if and only if the dictator is unpopular.  The opposition gets a payoff of 1 if it successfully challenges and 0 otherwise. The dictator gets a payoff of 0 if he is successfully challenged and a payoff of 1 otherwise.

(a)  Suppose there was no election. Under what conditions will the opposition challenge the dictator. Using a graph with η on the horizontal axis and γ on the vertical axis, show the region in which the opposition decides to challenge, and the region in which it does not. What is the dictator’s expected payoff in each of these regions? Provide some intuition for why the expected payoff differs across these regions.

(b)  Now consider a fair election without interference (ϕ = 0).  Suppose v = 1.  Using Bayes rule compute the posterior probabilities of θ conditional on v = 1, and then conditional on v = 0. For each case, v = 1 and v = 0, specify the opposition’s optimal challenge strategy. What is the dictator’s expected utility in this case?

(c)  Next, for any ϕ chosen, use Bayes rule to compute i) the posterior probability of the dictator being unpopular conditional on v = 1, ii) the posterior probability of the dictator being unpopular conditional on v = 0, and iii) the unconditional probability that v = 1 (that is, the dictator wins the election).

(d)  Consider two values of ϕ (ϕ = 0.1 and ϕ = 0.2) and see how the probabilities in the part above change. Do you see a tradeoff?

(e)  Suppose the dictators sets ϕ large enough so that 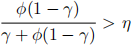.  What is the op- position’s optimal challenge strategy for v = 1 and for v = 0?  What is the dictator’s expected utility in this case?

(f)  Given the tradeoff in part (d) and the result in part (e), what is the optimal level of ϕ for the dictator? What is the gain in the dictator’s expected utility from manipulating the election compared to the fair election case?  How does this depend on λ (the likelihood of the dictator being popular) and η (how strong the opposition is)?