STAT 400, Spring 2024 Homework 09
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Homework 09
Due Tuesday, March 26, 11:59pm
STAT 400, Spring 2024
Each Exercise or lettered part of an Exercise is worth 5 points. Homework assignments are worth 50 points.
Exercise 1
Let X be a random variable that follows the Poisson distribution with mean λ, where λ > 0.
(a) What is the moment-generating function for X, a Poisson random variable? Derive the mgf using the definition and show your work.
(b) Find E[X] and Var[X] using the mgf of X found in part (a).
Exercise 2
Let X1, X2, … , Xn be an iid random sample of size n from a Poisson distribution with mean λ, where λ > 0.
(a) Find the method of moments estimator of λ, 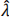 .
.
(b) Find the maximum likelihood estimator of λ, 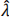 .
.
(c) Which of the estimators is unbiased for λ? The method of moments estimator (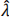 ), the MLE (
), the MLE (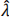 ), neither, or both?
), neither, or both?
Exercise 3
Let X1, X2,…, Xn be an iid random sample of size n from an Exponential(θ) distribution with probability density function
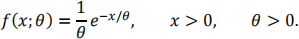
(a) Find the maximum likelihood estimator for θ, 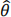 . Then using that result, calculate the estimate when x1 = 14, x2 = 25, and x3 = 18. (This will be a number.)
. Then using that result, calculate the estimate when x1 = 14, x2 = 25, and x3 = 18. (This will be a number.)
(b) The mean squared error (MSE) of an estimator 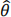 is defined as MSE(
is defined as MSE(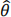 ) = [Bias(
) = [Bias(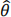 )]2 + Var(
)]2 + Var(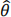 ).
).
Calculate the value of the bias of the maximum likelihood estimator for θ, 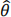 . (That will be a number.) Then calculate the mean squared error of
. (That will be a number.) Then calculate the mean squared error of 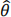 . (This will be in terms of θ.)
. (This will be in terms of θ.)
Exercise 4
Let X1, X2,…, Xn be an iid random sample where Xi ~ Normal(µ, σ2), µ unknown, and σ2 unknown.
In Discussion, two similar exercises were explored: finding the MLE for µ when σ2 was known, and finding the MLE for σ2 when µ was known. This time, both are unknown, but those Discussion exercises will still be helpful.
(a) Find the MLE’s for both µ and σ2.
Hint: The likelihood and log-likelihood functions for both will be the same. But when you get to Step 3, you’ll get two expressions: one from taking the derivative with respect to µ, and the other by taking the derivative with respect to σ2.
(b) Show that the MLE  is a biased estimator for σ2 when µ is unknown. Calculate the value of the bias of
is a biased estimator for σ2 when µ is unknown. Calculate the value of the bias of  .
.
(c) Based on your answer to part (b), what would you need to do to the MLE  to create an unbiased estimator for σ2 when µ is unknown? Show that your new statistic based on the MLE
to create an unbiased estimator for σ2 when µ is unknown? Show that your new statistic based on the MLE  is unbiased.
is unbiased.
Hint: What is the name/symbol of that “new statistic”? You have seen it before.
2024-03-29