Econ 101 Final exam 2008
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Econ 101
Final exam
June 11, 2008
Instructions. This is a 3 hour closed book/notes exam. There are 35 multiple choice questions (5 pages), each one represents 1.2 points (a total of 42 points). There are three short problems that count for the remaining 60 percent.
I. (20%) Taxation and government spending
Consider an economy in which households have a utility function given by
u(c, l) = ln(c)+ a ln(1 − l),
where c is consumption, l is labor supply, and a > 0. The household has one unit of time available so 1 − l is leisure. The production function for consumption goods is given by
y = wl,
where y is output, w > 0 is the wage, and l isthe labor demand. The government uses revenues from taxing households to pay for g. HINT: To help you with the computations, remember that the derivative of a logarithmic function is
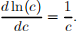
(a) Suppose that the government finances g through lump-sum taxes, where T is the lump-sum tax paid by the household. For a given g 持 0; determine consumption, output, and employment in equilibrium, and show how these quantities are affected by a change ing. Explain your results. HINT: Recall that labor-leisure decisions are made until MRsl,c = w.
ANS. The consumer solves
max ln(c)+ a ln(1 − l),
subject to
c = wl − T .
Substitute the budget constraint into the objective function to obtain
max ln(wl − T)+ a ln(1 − l),
the first order condition is
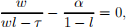
which can also be seen as coming from the MRsl,c = w. That is,
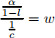
so
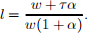
The market clearing conditions are
c + g = y ,
g = T .
The competitive equilibrium is
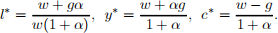
The response to changes in g are
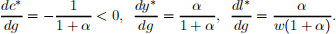
An increase ing drives up T and therefore reduces consumer’s income. Provided that c is normal good, c will go down. But the decrease in consumption is less than one-for-one in response to the increase ing, and since y = c + g; theny will increase. Leisure is also a normal good, the optimal level of 1 - l goes down with reduced income, therefore consumer’s labor supply increases.
(b) Suppose now that g is financed by a proportional tax on labor income. That is, let T be the tax on labor income, so that total taxes collected by the government equal 山lT; where 山 is the real wage. Write down the government’s budget constraint.
ANS. The government budget constraint is
g = wlT.
(c) For given g, solve for consumption, output, and employment in equilibrium, and show how quantities are affected by a change ing.
ANS. The consumer problem is
max ln(c)+ a ln(1 - l),
subject to
c = wl(1 - T).
Substitute the budget constraint into the objective function to obtain
max ln(wl(1 - T)) + a ln(1 - l),
the first order condition is
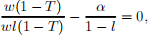
so
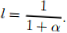
The market clearing conditions are
c + g = y = 山l,
g = wlT.
The competitive equilibrium is
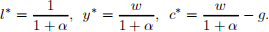
The response to changes in g are
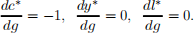
An increase in g doesn’t change the equilibrium employment and output, while it reduces the equi- librium consumption one-for-one. The reason is the following. Because of log preferences, income effect and substitution effect exactly offset each other, leaving labor supply and hence employment and output unchanged. Since c + g = y, private consumption has to be crowded out by public goods one-for-one.
II.(20%) Intertemporal consumption
Consider an intertemporal economy in which households have a utility function given by
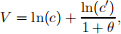
where c and c0 are consumption in periods one and two. Households have access to financial markets but their choices of consumption must satisfy the following budget equations:
c + s = y +(1+ T)b,
c' + b' = y' +(1+ T)s
with b as the household initial assets inherited from previous generations and with b0 as the bequests the current generation plans to leave. Savings are given by s and y and y0 are exogenous income in the current
and future periods. As usual, T is a rate of return per unit of time.
(a) Write the two budget equations as a single budget constraint.
ANS: As in class,
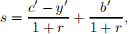
and therefore
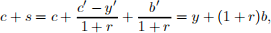
or
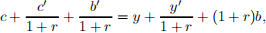
that becomes
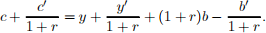
(b) Show that the marginal rate of substitution between current and future consumption is:
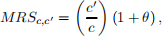
and remember that the optimal decisions are those in which MRSc,c' = (1+T). Show that consumption increases overtime if T > θ, and decreases overtime if T < θ. HINT: To help you with the computations, remember that the derivative of a logarithmic function is
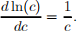
ANS: Using the hint provided above, the optimal decisions are implicit in the following equation:
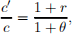
derived as in our PS 4. Since c = (1 + θ)/(1 + T)c', then T > θ implies c < c0 . That T < θ gives the opposite result is also easy to show.
(c) Using the budget constraint, find the levels of consumption in the current and future periods. Describe what is the response to an increase in the bequests received by parents, b. Briefly describe the response in consumption to a change in T. (You don’t need to provide explicit derivations for this question.)
ANS: To obtain consumptions notice that
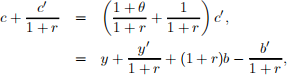
so
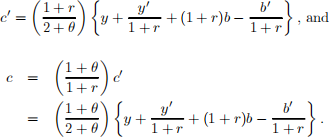
Therefore, an increase in b is a income effect that raises both consumptions. When r changes, there are income and substitution effects. If households are borrowers, an increase in risa negative income effect while if they are lenders there is a positive income effect. The substitution effect is always negative, i.e., reduces current consumption, but the overall sign is not determinate.
III. (20%) The Solow model
This question studies the Solow model of economic growth. Assume that the production function is Y = zF (K, N) = zK![]() N1-
N1- ![]() with z as total factor productivity, K as the capital stock in the economy, and N as the population of the economy. The evolution of capital is given by:
with z as total factor productivity, K as the capital stock in the economy, and N as the population of the economy. The evolution of capital is given by:
K' = I +(1 - d)K,
with I as total investment and d as the depreciation rate. Assume, as we did in class, that I = sY and that N0 = (1 + n)N.
(a) Show that income per worker y = Y/N is given by:
y = zk![]() ,
,
with k = K/N and that capital per capita changes according to:
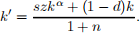
ANS. Divide both sides by N and obtain Y/N = zK![]() N1-
N1- ![]() /N = z(K/N)
/N = z(K/N)![]() = zk
= zk![]() . Recall that we can write K0 = I +(1 - d)K as K0 = sY +(1 - d)K. Divide both sides by N:
. Recall that we can write K0 = I +(1 - d)K as K0 = sY +(1 - d)K. Divide both sides by N:
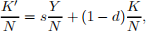
which can be written as
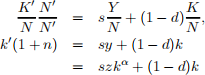
(b) Find the steady-state value for capital per capita, k* . In order to find the value of capital per worker
in the steady state, k* , recall that k = k0 = k* describes the steady state.
ANS. In the steady state, k0 = k, so we need to solve the following equation:
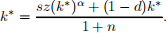
The solution leads to
k* (n + d) = sz(k* )![]() ,
,
and to
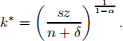
(c) Find income per capita in the steady-state and describe the effect of changes in s and non income per capita in the steady-state.
ANS. Income is just y* = z(k* )![]() . In particular, we know that
. In particular, we know that
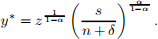
From here we can see that if n increases income declines and if s increases income increases.
(d) Find consumption in the steady-state. Find also the savings rate s that maximizes steady-state con- sumption.
ANS. Recall that
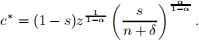
To maximize consumption, it is easier to take logs on both sides to obtain
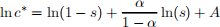
with A made of terms that are not related to s and hence are not relevant. Once the expression is in logs, it is easier to maximize. Take the derivative with respect to s and make it equal to zero. Clearly if s = 0 or s = 1 we have zero consumption. To find the maximum, take the derivative of the log function:
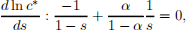
and from here we obtain s = a.
2024-03-20