MAST20030 Differential Equations
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MAST20030 Differential Equations
Question 1 (14 marks)
Consider the following IVP:
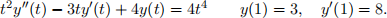
(a) Find a complementary solution y1(t) by trialling y1(t) = tn
(b) Use the result of (a) to solve (1) by means of reduction of order.
(c) Given y1(t), could you have used the wronskian to find the solution of (1)? Why?/Why not?
Question 2 (14 marks)
Consider the following system of linear ODEs
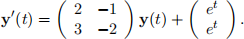
(a) Use diagonalisation to derive a decoupled system of first order linear ODEs.
(b) Solve the system of (a).
(c) Use the result of (b) to find the general solution of (2).
Question 3 (16 marks)
Consider the following second order linear ODE:
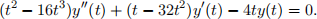
(a) Trial a power series
and show that the coefficients cj satisfy the recursion
Compute the first four series coefficients.
(b) Is the power series solution of (a) genuine? What is its radius of convergence?
(c) Given the results of (a) and (b):
(i) Do you expect there to be further linearly independent solutions of (3)? Why?/Why not?
(ii) If the answer to (i) is “yes”, name at least one method to obtain further solutions.
Question 4 (14 marks)
(a) Find the following (inverse) Laplace transforms.
(i)
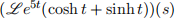
(ii)
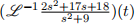
(b) Solve the following IVP:
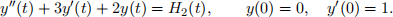
Question 5 (13 marks)
(a) Compute the eigensystem of the following BVP:
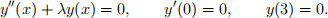
Normalise your eigenfunctions yn(x) by requiring that yn(0) = 1. Explicit calculation required! Do not quote results from the lectures.
(b) The eigenfunctions of (a) are orthonormal with respect to an inner product <f, g>. Give the definition of this inner product and show explicitly that <yn, yn> = 1 for the eigenfunctions yn of (a). You need not show that <ym, yn> = 0 for m
n.
Question 6 (20 marks)
Consider the two-dimensional Laplace equation

on a rectangle 0 < x < a, 0 < y < b. The boundary conditions are
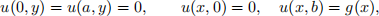
where g(x) is some function on 0 ≤ x ≤ a.
(a) Use separation u(x, y) = X(x)Y (y) to derive ODEs for X(x) and Y (y). Then solve the BVP for X(x) by giving its eigensystem. You may use results from the lectures for the second step but not for the first step.
(b) Solve the BVP for u(x, y) by expressing the series coefficients of the solution in terms of integrals containing g(x).
(c) Determine the solution of the BVP for the special case of

(d) Is the solution of (c) genuine? Why?/Why not?
Question 7 (9 marks)
Compute the Fourier transform of
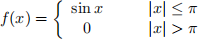
2021-11-02