Summative Assessment 2, ECON0125
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Summative Assessment 2, ECON0125
March 5, 2024
This homework is the second of the two that will determine the coursework part of your grade. Your grade will depend only on the maximum mark out of the two homeworks. Each question is split up into multiple parts. Some parts have been deliberately made substantially more difficult than others, so do not worry if you are not able to complete all of them.
Question 1 (Properties of Penalized Estimators)
Let Θ be some set of functions. Suppose for all θ ∈ Θ, P en(θ) ≥ 0. For any λ ≥ 0 and c ≥ 0 let us define estimators 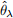 and
and 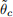 as below, where we assume that both optimization problems have unique global minima.
as below, where we assume that both optimization problems have unique global minima.

i. Consider some fixed λ ≥ 0. Define c(λ) = P en(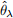 ). Show that
). Show that 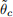 (λ) =
(λ) = 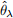 .
.
ii. Consider some fixed c ≥ 0. Suppose there exists a λ(c) so that P en(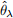 (c)) = c. Show that
(c)) = c. Show that 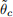 =
= 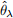 (c)
.
(c)
.
iii. In light of your answers to parts i. and ii. discuss how you can apply results like Proposition 1.5 for estimators that incorporate penalization.
Now let 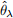 satisfy the following for some sample loss function
satisfy the following for some sample loss function 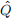 which need not be the sum of squared residuals:
which need not be the sum of squared residuals:
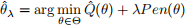
iv. Show that P en(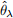 ) is weakly decreasing in λ.
) is weakly decreasing in λ.
v. Suppose that 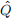 (θ) ≥ 0 for all θ ∈ Θ, Θ contains the zero function θ(x) = 0, ∀x (we will simply write θ = 0 in this case), and suppose P en(0) = 0. Show that for all λ > 0:
(θ) ≥ 0 for all θ ∈ Θ, Θ contains the zero function θ(x) = 0, ∀x (we will simply write θ = 0 in this case), and suppose P en(0) = 0. Show that for all λ > 0:
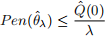
vi. Under the conditions of part v., what happens to P en(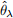 ) as λ → ∞?
) as λ → ∞?
Question 2 (IV Revisited)
Consider the LATE theorem on page 6 of the second set of lecture notes. Throughout this question, assume all of the conditions of that theorem hold.
i. Show that the following two equalities hold, where the random variable T is defined as on page 6.
P(T = a) = P(X = 1|Z = 0)
P(T = n) = P(X = 0|Z = 1)
ii. Show that the following equalities hold:
E[Y (1)|T = a] = E[Y |X = 1, Z = 0]
E[Y (0)|T = n] = E[Y |X = 0, Z = 1]
iii. Prove the following:
P(X = 1|Z = 1) = P(T = c) + P(T = a)
P(X = 0|Z = 0) = P(T = c) + P(T = n)
iv. Show that the following two equalities hold:
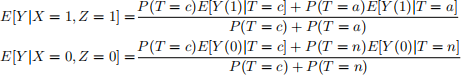
v. Using the results in parts i.-iv. solve for E[Y (0)|T = c] and E[Y (1)|T = c] in terms of directly observable quantities. (Note: you must show how your so-lution follows from the equalities in the previous parts of this question. Do not simply copy the formula in the lecture notes).
vi. In this setting, the ATE is in general not point-identified. Suppose Y is binary. Using the results above, identify scalars a > 0 and b < 1 so you can achieve upper and lower bounds on the ATE as follows:
a ≤ E[Y (1) − Y (0)] ≤ b
Try and find such an a and b so that b − a is as small as possible. When are your bounds more/less informative (i.e., when is b−a small/large)? Discuss.
Question 3 (Neyman Orthogonality)
Let Yi ∈ R be a measure of an individual i’s wealth and Xi ∈ 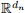 a potentially high-dimensional vector of individual characteristics that includes a constant. Assume
a potentially high-dimensional vector of individual characteristics that includes a constant. Assume 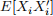 is non-singular. Let us consider a linear model for wealth with true parameters β0 ∈
is non-singular. Let us consider a linear model for wealth with true parameters β0 ∈ 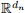 . To be precise, we consider the model below:
. To be precise, we consider the model below:

Note that, because Xi
includes a constant 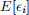 = 0. We are interested in asymmetry in the distribution of residual variation in wealth. More precisely, we wish to make inferences about the skewness of the residual
= 0. We are interested in asymmetry in the distribution of residual variation in wealth. More precisely, we wish to make inferences about the skewness of the residual 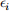 in the model above. That is, the parameter θ0 given by
in the model above. That is, the parameter θ0 given by 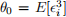 . We intend to estimate the high-dimensional parameters β0 using penalized regression. We then plan to use these first-stage estimates to obtain an estimate of the scalar parameter θ0 in a second stage.
. We intend to estimate the high-dimensional parameters β0 using penalized regression. We then plan to use these first-stage estimates to obtain an estimate of the scalar parameter θ0 in a second stage.
i. What is ‘Neyman orthogonality’? Why might it be relevant in the setting described above?
ii. Express β0 as the solution to a vector of moment conditions. That is, write down a score function ϕ so that E[ϕ(Yi , Xi ; β)] = 0 if and only if β = β0.
iii. Express θ0 as the solution to a simple moment condition that depends on β0. That is, write down a score function g so that E[g(Yi , Xi ; θ, β0)] = 0 if and only if θ = θ0.
iv. Is your moment condition in part iii. Neyman orthogonal with respect to β0? Does your answer depend on whether 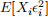 = 0?
= 0?
v. Construct Neyman orthogonal moments condition for θ0. That is, find a score 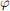 and a vector of additional nuisance parameters µ0 so that:
and a vector of additional nuisance parameters µ0 so that:

if and only if θ = θ0. And moreover:
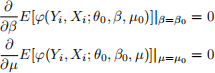
Note that there is more than one possible correct answer here.
2024-03-14