STAT 473/873 (Winter 2024) Assignment 3
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
STAT 473/873 (Winter 2024)
Assignment 3
The assignment is due on Mar. 14 (Thursday) at 8:00pm.
Place and instructions of submission: Submit to Crowdmark.
You can still submit your assignment after the scheduled submission deadline; the penalty for a late assignment is 1% per hour.
Watch out for a crowdmark techinical feature: If you have clicked submission before the deadline, then once the deadline has passed, you CANNOT resubmit or add more materials to the submission.
There are 3 problems.
If using R is required for a problem and code and output are long, please attach the code and output at the end of your solutions to the problem, as evidence of your independent work.
1. Suppose Yi , i = 1, . . . , n are independent response variables with probability mass func-tions
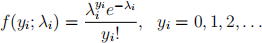
with parameter λi > 0. For each yi , there is a corresponding vector of explanatory variables xi = (1, xi1, . . . , xi,p−1)T, with p < n.
(a) Show that the distribution of Yi is in the exponential dispersion family and identify the parameters θi and ϕ, the functions ai(ϕ), b(θi), c(yi, ϕ) and the variance function V(µi).
(b) Use Theorem 3.2.1 to derive the mean and variance of Yi .
(c) Set up a regression model with the canonical link and specify the corresponding link function that links the mean of the response µi to the linear predictor ηi .
2. Suppose Yi , i = 1, . . . , n are independent response variables with density functions of the form
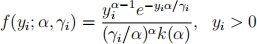
with parameters γi > 0 and α > 0, and k(α) is a known function of α. Associated with each yi is a vector of explanatory variables xi = (1, xi1, . . . , xi,p−1)T, with p < n.
(a) Show that the distribution of Yi is in the exponential dispersion family and identify the parameters θi and ϕ, the functions ai(ϕ), b(θi), c(yi, ϕ) and the variance function V(µi).
(b) Based on properties of the exponential dispersion family, derive the mean and variance of Yi in terms of γi and α.
(c) Set up a regression model with the canonical link and specify the corresponding link function that links the mean of the response µi to the linear predictor ηi .
(d) Assume that the parameters γ1 = . . . = γn = γ, while α is a known constant. Is 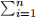 Yi a sufficient statistic for γ? Why?
Yi a sufficient statistic for γ? Why?
3. The number of deaths from leukemia and other cancers among survivors of the Hiroshima atom bomb are shown in Table 2 below, classified by the radiation dose received. The data refer to deaths during the period 1950-1959 among survivors who were aged 35 and 64 years in 1950 (Cox and Snell 1981, Otake 1979, Dobson and Barnett 2008).
When analyzing the data, for each radiation dose class, take the middle point of the dose interval as the dose value. That is, let dose = 5 for the 1-9 class, and dose = 30 for the 10-49 class, and so on, and let dose = 250 for the 200+ class.
Table 1: Deaths from leukemia and other cancers by radiation dose from the Hiroshima atomic bomb.
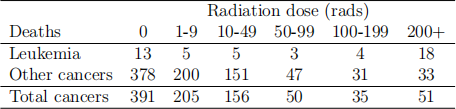
(a) Find a suitable model to describe the dose-response relationship between radiation and the proportion of death from leukemia among cancer mortality. Assess the fit of the models using the dose-response curve approach. Interpret your final model and results.
(b) Suppose a complementary log-log link regression is appropriate for the data. Estimate the dose value at which the proportion of death from leukemia reaches 10% of all cancer mortality.
2024-03-13