Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MATH-UA 253 and MA-UY 3204 (NYU Courant)

Spring 2024: Linear and Nonlinear Optimization

Assignment 3 (due Sunday Mar. 10, 2024 at 11:59pm ET)

1. [Complementary slackness, 3+1pts] Consider the LP (if you like you can consider this as the dual LP of a primal-dual pair in symmetric form):

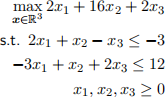
Check if any of the following is an optimal solution by using complementarity slackness.

• x = (6, 0, 12)

• x = (0, 2, 5)

• x = (0, 0, 6)

For what, if any, values of c1, c2 would x = (0, 0, 6) be an optimal solution?

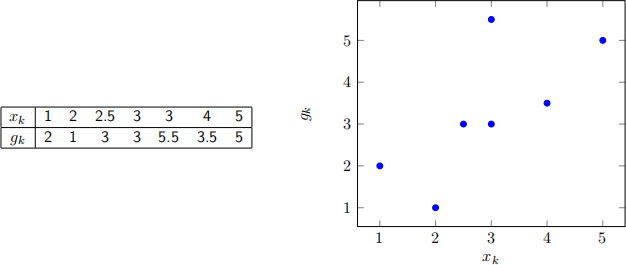
2. [L1 and L2 regression, 1+1+1pts] At points xk, we consider measurements gk given in the following table and shown in the figure:

We would like to fit a linear model (i.e., a line with parameters a, b) of the form

h(x) = a + bx,      a, b ∈ R

to this data, which minimizes the errors εk := h(xk) − gk between the model and the data. For that purpose we consider two optimization objective functions which we will minimize over the parameters a, b:

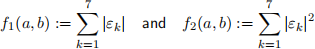
(a) Formulate the minimization problem with f1 as linear program, and solve it using Julia to compute (a1, b1). Sketch the resulting model h(·) (i.e., the line) into the figure (it’s OK to do this manually).

(b) Solve the minimization problem with f2, which is a parametric fitting problem using Julia to compute (a2, b2). This is not a linear program, so you can either do this using a nonlinear optimization solver in Julia, or easier, by solving the normal equations AT Ay = AT b, where

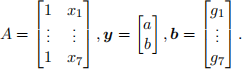
Again, sketch the resulting model line into the figure.

(c) Now assume that one measurement point got terribly corrupted, namely g5 = 100 instead of g5 = 5.5. Repeat solving the two optimization problems above and draw the model function h(·) you obtain from minimizing f1 and f2 into the figure. Which formulation is sensitive to corrupted data, and which is not?

3. [Simple network, 2+2pts] Consider the network shown below, which has 4 nodes and 4 arcs. Suppose there are sources (or supply) of magnitude 1 at nodes 1 and 4, and sinks (or demand) of −1 at nodes 2 and 3.

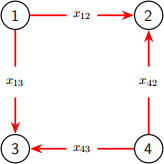
(a) Let x = (x12, x13, x42, x43) be the flows in the arcs, and let b = (b1, b2, b3, b4) be the vector of sources and sinks (using the book’s convention that sources are positive and sinks are negative). A flow is then admissible exactly if Ax = −b and x ≥ 0, Write down the matrix A and the vector b.

(b) We learned early in the semester how to find the extreme points of the set {Ax = −b, x ≥ 0} when A has full rank. But the matrix A associated with a network does not have full rank: since the rows of A sum to zero and the components of b sum to zero, the linear system Ax = −b in this problem provides only three linearly dependent relations on the components of x. Still, dropping the fourth equation (which expresses equilibrium at node 4), the rule we learned earlier can be applied to the remaining 3 equations. Use this rule to identify all extreme points of the feasible set.

4. [Shortest path theory, 3pt extra credit] In this problem we show theoretically that the shortest path can be found by solving a network flow LP. To understand where the dual problem comes from and give you some intuition, you can watch this youtube video: https://www.youtube. com/watch?v=2XRSxa03V5g.

Many applications call for finding the shortest (or minimum travel time) path between two nodes of a network; for example, when Google Maps gives you directions it is doing something like that. This problem and the next one explore how this problem can be solved using linear programming. (There are also other methods, which tend to be more efficient for large graphs; still, this is an elegant application of LP.) This problem covers the theory, while the next one considers a numerical example.

Consider a network in which the N nodes represent locations and the “cost” cij assigned to the directed arc from node i to node j (if it exists) is the travel time required to get from i to j by that arc. (We assume that all travel times are strictly positive.) Given two particular nodes (say, node 1 and node N), we want to find the minimum travel time and an optimal path from node 1 to node N. (We assume it is possible to get from 1 to N on the given network.) Let’s show this can be done by using the simplex method to minimize 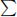cijxij subject to xij ≥ 0 and the usual network equilibrium constraints, with a unit source at node 1, a unit sink at node N, and no other sources or sinks.

(a) To start, show that if a path from 1 to N on the network never repeats any node then taking xij = 1 on the arcs in the path and xij = 0 elsewhere gives a feasible point for this LP. Thus the optimal value of the LP is less than or equal to the min travel time. Our task is to show that it’s not smaller, and that an optimal x found by the simplex method (which has integer entries, by the integrality theorem) is of the type just considered.

(b) Show that the dual problem maximizes yN −y1, subject to yj −yi ≤ cij when there’s an arc from i to j. Also, show that complementary slackness says an optimal x* and an optimal y* must have 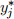 − 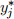= cij whenever 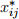≠ 0. Finally, explain why we may without loss of generality take 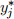to be 0.

(c) Observe that if x* comes from a path as in (a), then 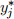 at each node along the path would be the travel time from node 1 to node i. So given x*, it is natural to seek an associated path (going from node 1 = p1 to node p2 to node p3, etc, until it arrives at node N) as follows:

• At node 1, there must be at least one departing arc with a nonzero flow (why?). If there is more than one such arc, choose one, and let p2 be its destination. Notice that the value of y* at node p2 is c1p2.

• At node p2 we repeat this process: there must be a departing arc with a nonzero flow (why?). If there is more than one such arc, choose one, and let p3 be its destination. Notice that the value of y* at node p3 must be c1p2 +cp2p3 . Since the cij are all positive, p3 cannot be one of the nodes that the path has already visited.

• Continuing this process: it must arrive in at most N steps at node N (why?).

Let x′ be the flow associated with the resulting path (as in part (a)). Show that x′ = x*, by arguing that if they were different then x ∗ would not have been optimal. (You’ll need to use the integrality theorem, which is available provided that x ∗ is obtained using the simplex method.) Conclude that a solution of the proposed LP, if obtained by the simplex method, must be associated with a minimal-travel-time path from node 1 to node N.

5. [Shortest path example, 3pt] Continuing from previous problem, let’s implement the proposed method numerically for the network shown in the figure below, if each arc has the same travel time (cij = 1) and we want to travel from node 1 to node 4. (The minimum time for this example is, of course, immediately evident: it is 2, and there are two optimal paths, namely 1 → 2 → 4 and 1 → 3 → 4.)

(a) If the flows are x = (x12, x13, x24, x34) and b = (1, 0, 0, −1), then the admissible flows are those satisfying Ax + b = 0 and x ≥ 0. What is the matrix A?

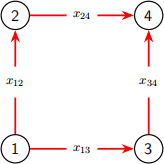
(b) Solve the linear program suggested by problem 3 numerically, using GLPK. Does it get the minimum travel time right? What path does it give?

(c) Now solve the same linear program numerically using Ipopt (which is solving linear programs using something other than the simplex method). Your answer will be very different. Does it get the minimum travel time right? Does it provide an optimal path?

6. [The Game of Morra, 5pts] Two players simultaneously throw out one or two fingers and call out their guess as to what the total sum of the outstretched fingers will be. If a player guesses right, but his opponent does not, she receives payment equal to her guess. In all other cases, it is a draw.

(a) List the pure strategies for this game.

(b) Write down the payoff matrix for this game.

(c) Formulate the row player’s problem as a linear programming prob- lem. (Hint: Recall that the row player’s problem is to minimize the maximum expected payout.)

(d) What is the value of this game?

(e) Find the optimal randomized strategy.