COMP 3621 (Winter 2024) Advanced Data Structures Assignment 3
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
COMP 3621 (Winter 2024)
Advanced Data Structures
Assignment 3
Deadline: Sunday, March 2, by 9:00pm
Submission: For Question 1, upload a PDF. For Question 2, zip together your Java files +README.txt, and upload this ZIP file to Moodle.
1. A Java ArrayList is an implementation of the List interface that uses an array “under the hood.” If this array is full when the add method is called (the add method inserts an element into the next free spot in the array), a new array of twice the length is allocated (***), the values in the old array are copied into the new array, the item passed to add is added to the new array, and the old array is discarded (i.e., garbage collected). This means that sometimes add is cheap (constant time) and sometimes it is expensive (linear in the number of list elements). However, if we start with an empty list and an underlying array of length 1, and then perform a sequence of n add operations, the average (amortized) cost of all these add operations is low. Derive the tightest possible upper bound on this amortized cost as a function of n.
For this question, don’t use Big-O (or Big-Theta or Big-Omega). Instead, count the exact number of array assignments (but no other operations). A single array assignment occurs when a new value is inserted into the next free position in an array, and 2k array assignments occur when the contents of a full array of size 2k are copied into the first half of a new array of size 2k+1. You can take advantage of the fact that it suffices to limit consideration to values of n that maximize the amortized cost (since your goal is an upper bound).
(***) Actually, this isn’t exactly what happens. In practice, a new array that is 50% larger is allocated, but for the purposes of this question, it’s simpler to assume that the new array is twice the size of the old one.
2. Here is your challenge for this part of the assignment: Given an undirected graph G and an integer k ≥ 1, count the number of pairwise non-isomorphic induced subgraphs of G with k vertices.
Definitions
The opening description might require further explanation. First of all, we need the idea of a graph isomorphism. Two undirected graphs G and H are isomorphic (“have the same shape”) if they are essentially the same graph, but possibly with different labels on the vertices, and possibly drawn differently. For example, the two graphs in Figure 1 are isomorphic, even though they look very different. The reason is that there exists a bijective function f that maps the node labels of G to the node labels of H such that there is an edge between nodes x and y in G if and only if there is an edge between f(x) and f(y) in H. Put another way, two graphs are isomorphic if the
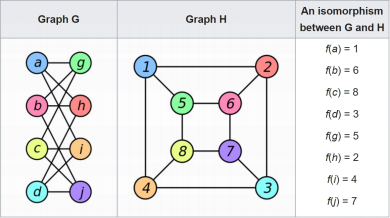
Figure 1: Two isomorphic graphs with 8 vertices. (Images by Booyabazooka, Wikimedia Commons, CC BY-SA 3.0.)
nodes of one graph can be rearranged so that the two graphs look identical (ignoring node labels). A necessary condition, of course, is that two isomorphic graphs must have the same number of nodes.
Now we need the idea of a subgraph. Given a graph G = (V, E) (where V is the set of vertices/nodes of G, and E is the set of edges of G), a subgraph of G is a graph G′ = (V ′, E′) that is formed by taking a subset V ′ of the nodes of G (i.e., V′ ⊆ V) and a subset E′ of the edges of G (i.e., E′ ⊆ E), with the restriction that any edge in E′ must connect two nodes in V ′ . In other words, we form a subgraph of G by choosing any set of nodes in G, and then choosing zero or more edges in G, as long as each edge we choose joins two of the chosen nodes. Note that V ′ could be the empty set, in which case the subgraph is the empty graph (clearly an edge case, no pun intended), or, at the other extreme, V′ could be all of V.
Finally, we need the idea of an induced subgraph. Given a graph G, an induced subgraph is formed by choosing a subset of the nodes of G, and then choosing every edge in G that joins two of the chosen nodes. This means that an induced subgraph is completely determined by the set of chosen nodes, since there is no choice about which edges to include.
Back to the task at hand . . .
The original statement of your challenge should now make a lot more sense. Given an undirected graph G and an integer k ≥ 1, you basically need to find all induced sub-graphs of G with k nodes, and then keep only one induced subgraph in each isomor-phism class, i.e., keep the maximum number of induced subgraphs such that no two of these subgraphs are isomorphic to each other (they are pairwise non-isomorphic). Actually, you only need to compute the number of pairwise non-isomorphic induced subgraphs, but generating them might be a good way to go about this. (If you can figure out how to count them without generating them, that’s often ideal.)
Required Program
Write a Java program (decently commented) to meet this challenge. As in Part 2, you have freedom in how you structure your program, but make sure to follow these general guidelines:
(a) Use multiple classes if/when appropriate, and give your classes sensible names.
(b) Place a main method in a class by itself. The main method should prompt the user for the name of an input file specifying an undirected graph, and should also prompt the user for a positive integer k. It should then launch the rest of the program.
(c) You don’t need to produce an output file. Instead, the main method should just print a line containing the answer (make the output meaningful; don’t just print a number by itself).
(d) As you have done for before, include integrity checks in appropriate places (avoiding magic numbers) to ensure that references are non-null, values are in correct ranges, etc., potentially throwing IllegalArgumentExceptions.
(e) Carefully describe the structure of your program in a file named README.txt.
Input File Structure
You can assume that any input file specifying a graph will be structured as follows:
• The first line contains two space-separated integers, n and m, where 1 ≤ n ≤ 50 is the number of nodes and m is the number of edges (so what are the bounds on m?).
• This is followed by m lines, each of which contains two space-separated integers, x and y, indicating that there is an (undirected) edge between x and y. As is standard, nodes are indexed 0, 1, . . . ,(n − 1), so both x and y must be in this range.
• No edge is given more than once, and there are no self-loops.
Note that your challenge is (as far as I know) a computationally hard problem, which is why the maximum number of nodes is low. For the same reason, you may only be able to work with small values of k.
Simple Examples
(a) Suppose the input graph is any graph with at least one edge that is not a complete graph, and k = 2. Then the answer is 2.
(b) Suppose the input graph is a complete graph with at least 2 nodes, and k = 2. Then the answer is 1.
2024-03-06