Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MATH 135 Fall 2021: Written Assignment 5

Q1. (5 points)

(a) (1 mark) Let n be a nonnegative integer. Evaluate

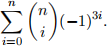
(b) (1 mark) Let n be a nonnegative integer. Evaluate

(c) (3 marks) Suppose that, for some integer n ≥ 3, when (2 + 3x)ⁿ is expanded, the coefficient of x³ is 3 times the coefficient of x2 . Determine the value of n.

Q2. (5 marks) Let a be an integer, and let S = {3, 5, 7, 11, . . .} be the set of odd prime numbers. Let T = {x ∈ Z : x (3a³ − a)} and let W = {x ∈ Z : x (7a³ + 3a)}. Show that

Hint: You can make use of the following fact (which is known as Euclid’s Lemma) without proof: For all integers a, b and every prime number p, if p | (ab), then p | a or p | b. You will see Euclid’s Lemma later in this course (Section 6.7 of the course notes).

Q3. (4 marks)

(a) (3 marks) Prove that {5a + 7b : a, b ∈ Z} = {2c + 3d : c, d ∈ Z}.

(b) (1 mark) The set(s) in part (a) is very special. What set is it?

Q4. (5 marks) The Fibonacci sequence f1, f2, . . . is defined by f1 = 1, f2 = 1, and fm = fm−1 + fm−2 for m ≥ 3. Prove that, for every natural number n, gcd(fn, fn+1) = 1.

Q5. (5 marks) Prove or disprove each of the following.

(a) (1 mark) For all integers a, b and c, gcd(ac, bc) = c · gcd(a, b).

(b) (4 marks) For all integers a, b and c, if gcd(b, c) = 1, then gcd(a, bc) = gcd(a, b) gcd(a, c).

Hint: You can use without proof the fact that, for all s, t, u, v ∈ Z, if s | u and t | v, then (st) | (uv).