ECON 4000 - Advanced Microeconomics Problem Set 1 Spring 2024
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Problem Set 1 - Deadline: Feb 19th, 2024, 23h:59m
ECON 4000 - Advanced Microeconomics
FSS - ECON
Spring 2024
Problem 1 [15 points]
Consider the following marriage market:
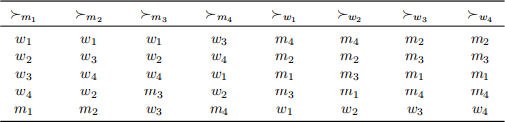
1. Find the men-proposing DA matching.
2. Find the women-proposing DA matching.
Consider the matching 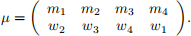
3. Is µ individually rational? If not, find all blocking agents (Note that there may be multiple blocking pairs).
4. Is µ stable? If not, find all blocking pairs (Note that there may be multiple blocking pairs).
Problem 2 [15 points]
Consider the following house allocation problem
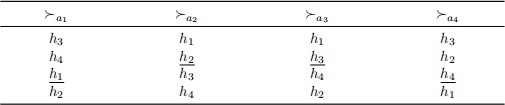
where the underlined houses show a matching, denoted by µ.
Let a priority π = (a2, a3, a4, a1) be given. (That is, for example, a2 π a3)
1. Calculate the matching SDπ (≻) selected by the serial dictatorship mecha-nism induced by π - when the preference profile ≻ in the above table are reported.
2. Does the matching SDπ (≻) Pareto dominate µ ?
Let a priority π′ = (a3, a1, a4, a2) be given.
3. Calculate the matching SDπ′ (≻) selected by the serial dictatorship mecha-nism induced by π′ - when the preference profile ≻ in the above table are reported.
4. Does the matching SDπ′ (≻) Pareto dominate µ ?
5. Suppose that true preferences are known to be ≻ as in the above table. Now agent a3 is trying to manipulate the serial dictatorship mechanism SDπ by reporting her false preference ≻′ a3 : h2, h3, h1, h4, while the other agents remain truthful. What is the resulting outcome? Is his attempt successful?
Problem 3 [20 points]
Consider the following housing market

where we denote the initial endowment (i.e., house ownership) by 
1. Find the matching T T C(≻) induced by the top trading cycles mechanism at ≻.
2. Does the matching T T C(≻) Pareto dominate the initial endowment µ ?
3. Verify that the matching T T C(≻) is individually rational and Pareto efficient.
4. Suppose that the true preferences are known to be ≻ as in the above table. Now agent a4 is trying to manipulate the TTC by reporting her false preference ≻′ a4 : h7, h3, h1, h4, while the other agents remain truthful. What is the outcome now? Is his attempt successful? Why?
Problem 4 [15 points]
A university has athletes and coaches, where each coach trains one athlete, each athlete has a preference over which coach they are trained by, and each coach has preferences over the athletes he or she will train. Suppose there are four coaches (c1, c2, c3 , and c4) and five athletes (a1, a2, a3, a4 , and a5). Their preferences are as follows (every athlete prefers to be matched to a coach than remaining unmatched):

1. What is the coach-optimal stable matching?
2. What is the athlete-optimal stable matching?
In any mechanism that produces a stable matching for a marriage market, no manipulation by men can ever result in him obtaining an outcome better, under his true preference, than the one he obtains under the men-optimal stable matching. In light of this, answer the following question:
3. Suppose the policy is that we use the coach-optimal stable matching. Who, if anyone, among the coaches and athletes can benefit from not saying their true preferences? If you say someone can benefit from not telling the truth, provide the alternative preference that they can tell to be better off than telling the truth.
Problem 5 [15 points]
In a research institution, any researcher can collaborate with any other researcher.
We can denote by R the set of all researchers.
A collaboration is then a function µ : R → R such that for each pair r, s ∈ R if µ(r) = s then µ(s) = r. Each r ∈ R has a preference over all researchers, including themselves.
Stability still applies here. Given a preference profile ≻, a researcher r blocks a collaboration µ if r ≻r µ(r). A pair (r, s) blocks µ if s ≻r µ(r) and r ≻s µ(s).
Unfortunately, there isn’t always a stable collaboration in this model. Below is a preference profile for three researchers. Use that profile to show that there is no stable collaboration.”
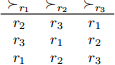
Problem 6 [20 points]
Consider a marriage market in which the number of men equals the number of women (|M| = |W| = n), every woman is deemed acceptable by men, and every man has the same preference over women. That is, for every m, m′ , ≻m=≻m′ .
1. Show that the outcome of the men-proposing deferred acceptance is the same outcome that would be produced by a serial dictatorship in a housing allocation model in which women are the agents, men are houses, and the priority π is such that if w ≻m w′ (remember that every man has the same preference over W, and therefore this can be any man m), then w π w′.
2. How many stable matchings are there in this market? Explain your response formally. (Note: when we say “this market” we mean any market satisfying the assumptions in this question.)
2024-03-03