LH Decision Theory and Games Assignment
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
LH Decision Theory and Games
Assignment
The assessment is four pages and there are six questions in total. Answer all questions.
The first five questions are problems. You need to show all steps in computations, and explain your steps. Individual marks for the parts are indicated in brackets.
The last question is an essay type question with a word limit of 500 words excluding references.
You are allowed to handwrite mathematical solutions and draw diagrams where rele-vant, and insert these as scanned pictures in your answers. Everything else should be typed. Word documents and PDFs are both acceptable.
I recommend the use Overleaf (www.overleaf.com) to type-set the document in Latex.
Question 1: Auctions (20 points)
Sebastian wants to sell a painting made by his mom.
There are 10 buyers interested in buying the painting, each one has their own pri-vate willingness to pay for the painting vi for i = {1, . . . , 10} which is known to be independently drawn from a continuous uniform distribution between [0, 1].
As Sebastian knows auction theory, he decides to run a first price sealed-bid auction.The buyer with the highest bid gets the painting and pays her/his bid. If there is any tie between the bids the painting is allocated at random between the buyers with the same highest bid.
1. Show that b(vi) = 10/9vi is a best-response to itself and explain your answer. (10 points)
2. Characterize Bayesian Nash Equilibrium (BNE) of this game and explain why the BNE that you are proposing is an actual equilibrium. (5 points)
3. Discuss two additional real examples of first price sealed-bid auction which are not mentioned in the lectures, originality of the examples will be taken into account. (5 points)
Question 2: 2×2 game (10 points)
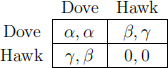
such that γ > α > β > 0.
1. Find the Nash equilibria in pure strategies and explain your answer.(2 points)
2. Find the Nash equilibrium in mixed strategies and explain your answer. (4 points)
3. Show that no one has an incentive to deviate from your proposed equilibrium in mixed strategies. (4 points)
Question 3: Linear public goods game (20 points)
N = {1, 2, 3, 4, 5, 6, 7} players are endowed with X tokens. Each player secretly chooses how many of their private tokens xi to put into a public pot. The tokens in this pot are multiplied by a factor α and this ”public good” payoff is evenly divided among players. Each player also keeps the tokens they do not contribute. Therefore, the expected payoff for every player i is
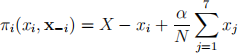
1. Show that if α = 4 then xi = 0 is a strategy Nash equilibrium and explain your answer. (5 points)
2. Show that if α = 10 then xi = X is a strategy Nash equilibrium and explain your answer. (5 points)
3. Explain why the values of α (i.e., greater or lower than N) change the type of Nash equilibrium than we can expected. (4 points)
4. Give an example of a real situation where we can expect 0 < α < N, originality of the examples will be taken into account. (3 points)
5. Give an example of a real situation where we can expect N < α, originality of the examples will be taken into account. (3 points)
Question 4: A war of attrition (10 points)
Two players are involved in a dispute over an object. The value of the object for both players is the same and equal to v.
Time is modelled as a continuous variable that starts at 0 and runs indefinitely. Each player chooses when to concede the object to the other player; if the first player to concede does so at time t, the other player obtains the object at that time.
If both players concede simultaneously, the object is split equally between them, player i receiving a payoff of 2/v. Time is valuable until the first concession each player loses one unit of payoff per unit of time.
1. Formulate this situation as a strategic game. (2 points)
2. Show that a strategy profile t = (ti,tj ) such that 0 < tj < ti cannot be a Nash equilibrium and explain your answer.(4 points)
3. Show that a strategy profile t = (ti,tj ) such that 0 < tj = ti = t cannot be a Nash equilibrium and explain your answer. (4 points)
Question 5: Contest to seize a land (15 points)
Suppose two armies are poised to seize a piece of land. Each army’s general can choose to attack, denoted by A, or not attack, denoted by N.
Each army can be of two types, strong (s) or weak (w). Each army (and its general) knows its type but not the type of the other. The probability that an army is strong is µ, where 0 < µ < 1.
The payoffs are as follows. The land is worth L. An army can capture the land if it attacks and its rival doesn’t or if both attack and it is strong while the other is weak.
If two armies of equal strength attack then neither captures the island.
Each army has a cost of fighting, denoted by ct where t denotes an army’s type. We assume that cs = 1, cw = 3, and L = 6. Note that there is no cost of attacking (fight-ing) if the rival does not attack (so think of ct as fighting cost rather than (military) expedition cost).
1. Show that (Ns, Nw), (As, Aw) and (Ns, Aw) cannot be a BNE in pure strategies. (7.5 points)
2. Show that (As, Nw) is a BNE in pure strategies if µ ∈ [3/2, 7/6]. (7.5 points)
Question 6: Discussion (25 points)
Using a game theoretical framework (describing the players, information sets, actions, and payoffs) explain in no more than 500 words the behavior of candidates prior to democratic elections?
2024-03-02