Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

Maths 130

Assignment 3

This assignment was written by Paddy (padraic.[email protected]); it consists of five prob-lems, worth a total of 35 marks.

If you want to use any results from class/the coursebook, you are welcome to do so without proof; just cite the result you’re after. (E.g. “As we saw in lecture on day X, we know that any convergent sequence must be bounded.”) Results from outside of this class should be avoided; if you really want to use them, though, you should both cite where your result comes from and reprove it fully in your own words before using it.

Upload your problems as one single .pdf file to Canvas before the assignment’s due date. Show all of your working, and justify your claims; problems that do not show their work or clearly explain their reasoning may receive reduced marks.

While you are allowed (and indeed encouraged!) to work with others on this course, everything you submit in this assignment must be written up by yourself in your own words. That is: you can talk about your ideas with others, but your writeups must be done on your own, and you should only write down arguments that you yourself fully understand. In particular, posting assignment questions or solutions online is a breach of the University’s academic integrity policies, and will be treated as such.

Instead, if you’re stuck on problems, please talk to us! You can ask for hints on Piazza, email your instructors, or stop by the online Maths Assistance Room. We are glad to work with you to help you succeed.

Finally, have fun!

1. (Mean value theorem.) We say that a function f has a fixed point at c if f(c) = c. [7 marks]

(a) Let f be a function that is differentiable on all of R, with n distinct fixed points. Explain why there must be at least n − 1 distinct values of c such that f’(c) = 1.

(b) Let f be a function that is differentiable on all of R, such that f’(x) < 0.5 for all x. Show that f has at most one fixed point.

2. (Optimization.) Congratulations; you’re a Pokemon trainer! As such, you have a Pikachu that you’ve been training so that you can be the very best.

The land outside of your town is infested with Spearow; to prepare for the attacks you’ll face when you leave the town, you’ve been improving your Pikachu’s health (H) and defense (D) values. You have 200 points to spread out between these two stats: that is,  When you leave the town, you know that the number of attacks you can take from Spearow on the way to the next town is approximately

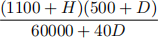
What should you make H and D equal to to maximize the number of attacks you can handle? What is the maximum number of attacks you can encounter?

3. (Derivatives of functions in two variables.) In class, we said that if f is “reasonably nice,” the directional derivative can be calculated by using the gradient of f, via the equation  This problem explores what happens if f is not reasonably nice.

Let be defined as follows:

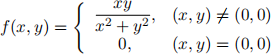
(a) Calculate  by using the limit definition of the derivative (see lecture / page 119 of your coursebook.)

(b) Calculate  again in the manner done above.

(c) Using your answers above, calculate

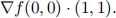
(d) Now, calculate directly via the definition (e.g. page 119.) Does your answer agree with what you derived in (c)?

4. (The fundamental theorem of calculus.) Suppose that is a continuously differentiable function on all of R with the following properties: for all  and  for all x. 

(a) What is f’(x)?

(b) Using this fact, what is f(x)?

5. (Antidifferentiation / integration.)