MSAE 4215 Midterm 1, Take-home exam 2024
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MSAE 4215
Midterm 1, Take-home exam
Feb 19, 2024
A very thin cable, length Lc, is suspended between two points at (xL, yL) and (xR, yR). The length of the cable LC is longer than the distance between points 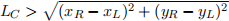 , so that the cable droops due to gravity, which acts on
, so that the cable droops due to gravity, which acts on 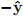 with acceleration g. The cable is assumed to be thin and flexible enough that it cannot support shear stresses transverse to its length, so that it could be conceptualized as an inextensible chain, formed by many hinged links which are free to rotate with respect to each other.
with acceleration g. The cable is assumed to be thin and flexible enough that it cannot support shear stresses transverse to its length, so that it could be conceptualized as an inextensible chain, formed by many hinged links which are free to rotate with respect to each other.
• In the first part (80 points), using the Cauchy equations at equilibrium,

you will derive a differential equation which describes the profile of the cable, y = y(x) (z = 0). To do this, use a parametric equation in terms of coordinate s along the cable (which integrates to LC),

with (tangent) length direction 

defined by a local angle θ = θ(s),
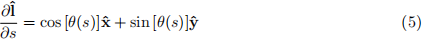
so that the slope at any point on the cable is

Denote ˆn(s) as the normal to the line vector at any point s, i.e. 
• In the second part (20 points), you will attempt to solve the differential equation for the specific, symmetric case

where h is the height of the pinned points (which are free to rotate, exerting only tension) above the lowest point on the cable at y = 0.
Important: Answer each subquestion a,b,c, following its specific instructions, before proceed-ing to the next subquestion, and indicate the answer to each subquestion clearly. Do not combine answers, and do not use another approach to the problem besides the one suggested, except (op-tionally) to check your work.
1. Differential equation
(a) In the (l, n) coordinate system, a) which elements of the 2D stress tensor σll, σnn, σln are nonzero, b) which elements are zero, and c) what sign do the nonzero stresses have?
(b) Write Cauchy’s equations for σxx and σyy in xy
(c) Transform σxx and σyy to the one nonzero component of stress in the (l, n) coordinate system; denote this nonzero component as σ.
(d) Express the Cauchy equations in terms of two equations relating θ, σ,(∂θ/∂s),(∂σ/∂s).
(e) In your previous answer, identify a quantity in terms of σ, θ which is invariant as a function of s; designate it as σ0, a constant.
(f) Eliminate σ and ∂σ/∂s and derive a first-order differential equation for the cable relating ∂σ/∂s and θ to constants. Group constants on the right hand side of the expression and express them as κ 2 =.
(g) Show that your first-order differential equation in θ and s, equal to constant κ 2 , is equiv-alent to a second-order differential equation,

Hint: you may find it useful that

(h) Give the general solution for the differential equation 25 in terms of κ and constants to be determined by boundary conditions; you might find symmetric and antisymmetric combinations (about x = 0). Hint: recall the definitions cosh x = (e x + e−x ) /2, sinh x = (e x − e−x ) /2
2. Specific solution
(a) For the case described, express the profile y = y(x) in terms of two constants, plus κ.
(b) Relate these constants to the given parameters for the problem: h, L, and LC; what constrains the shape? (Closed-form expressions might not be easy to find; it is OK to leave expressions unevaluated.)MSAE 4215 Midterm 1, Page 3 of 3 Feb 19, 2024
(c) Sketch the cable profile for h = L/4, and estimate the constants (to two or three significant digits) in terms of L.
2024-02-22