CSE 5523: Machine Learning - Homework #2
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
CSE 5523: Machine Learning - Homework #2
Due: 11:59pm 03/05/2024
Homework Policy: Please submit your solutions in a single PDF file named HW 1 name.number.pdf (e.g., HW 1 zhang.12807.pdf) to Carmen. You may write your solutions on paper and scan it, or directly type your solutions and save them as a PDF file. Submission in any other format will not be graded. Working in groups is fine, but each member must submit their own writeup. Please write the members of your group on your solutions. For coding problems, please append your code to your submission and report your results (values, plots, etc.) in your written solution. You will lose points if you only include them in your code submissions.
1) Softmax Regression [20 points].
In this problem, you will generalize logistic regression (for binary/2-class classification) to allow more classes (> 2) of labels (for multi-class classification).
In logistic regression, we had a training set {(ϕ(xn), yn)} of N examples, where yn ∈ {0, 1}, and the likelihood function is
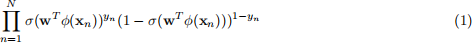
Now we generalize the logistic regression to multi-class classification, where the label y can take on K different values, rather than only two. We now have a training set {(ϕ(xn), yn)} of N examples, where yn ∈ {0,1, ..., K-1}. We apply a softmax transformation of linear functions of the feature variables ϕ for the posterior probabilities p(Y = k|ϕ), so that
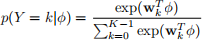
where wk are the parameters of the linear function for class k, and  are the parameters for softmax regression. The likelihood function is then given by
are the parameters for softmax regression. The likelihood function is then given by

where 1(.) is an indicator function so that 1(a true statement)=1 and 1(a false statement)=0. In the likelihood function, 1(yn = k) returns 1 if yn equals k and 0 otherwise.
(a) Gradient descent for softmax regression. We can optimize the softmax regression model in the same way as logistic regression using gradient descent. Please write down the error function for softmax regression E(w) and derive the gradient of the error function with respect to one of the parameter vectors wj , i.e. ∇wjE(w). (Show your derivation and final result using the given notations. The final result should not contain any partial derivative or gradient operator.)
(b) Overparameterized property of softmax regression parameterization and weight decay. Softmax regression’s parameters are overparameterized, which means that for any hypothesis we might fit to the data, there are multiple parameter settings that result in the same mapping from ϕ(x) to predictions. For example, if you add a constant to every w, the softmax regression’s predictions does not change. There are multiple solutions for this issue. Here we consider one simple solution: modifying the error function by adding a weight decay term,  :
:

For any parameter λ > 0, the error function Eλ (w) is strictly convex, and is guaranteed to have a unique solution. Similarly, please derive the gradient of the modified error function Eλ (w) with respect to one of the parameter vectors wj , i.e. ∇wjEλ (w). (Show your derivation and final result using the given notations. The final results should not contain any partial derivative or gradient operator.)
2) Support Vector Machine (10×8 points).
Recall that maximizing the soft margin in SVM is equivalent to the following minimization problem:
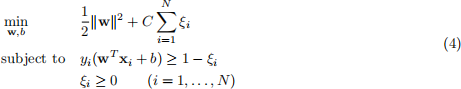
Equivalently, we can solve the following unconstrained minimization problem:

(a) Prove that minimization problem (1) and (2) are equivalent.
(b) Let (w* , b* , ξ *) be the solution of minimization problem (1). Show that if ξi* > 0, then the distance from the training data point x (i) to the margin hyperplane yi((w*) T x + b ∗ ) = 1 is proportional to ξi*.
(c) The error function in minimization problem (2) is
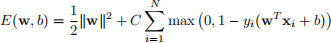
Find its derivatives: ∇wE(w, b) and ∂b/∂E(w, b). Where the derivative is undefined, use a subderiva-tive.
(d) Implement the soft-margin SVM using batch gradient descent. Here is the pseudo code:
Algorithm 1: SVM Batch Gradient Descent
w* ← 0 ;
b* ← 0 ;
for j=1 to NumIterations do
wgrad ← ∇wE(w*, b*) ;
bgrad ← ∂b/∂E(w*, b*) ;
w* ← w* − α(j) wgrad ;
b* ← b* − α(j) bgrad ;
end
return w∗
The learning rate for the j-th iteration is defined as:
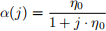
Set η0 to 0.001 and the slack cost C to 3. Show the iteration-versus-accuracy (training accuracy) plot. The training and test data/labels are provided in digits training data.csv, digits training labels.csv, digits test data.csv and digits test labels.csv.
(e) Let
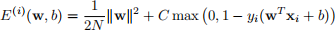
then

Find the derivatives ∇wE(i) (w, b) and ∂b/∂E(i) (w, b). Once again, use a subderivative if the derivative is undefined.
(f) Implement the soft-margin SVM using stochastic gradient descent. Here is the pseudo-code:
Algorithm 2: SVM Stochastic Gradient Descent
w* ← 0 ;
b* ← 0 ;
for j=1 to NumIterations do
for i = Random Permutation of 1 to N do
wgrad ← ∇wE(i) (w*, b*) ;
bgrad ← ∂b/∂E(i) (w*, b*) ;
w* ← w* − α(j) wgrad ;
b* ← b* − α(j) bgrad ;
end
end
return w∗
Use the same α(·), η0 and C in (d). Be sure to use a new random permutation of the indices of the inner loop for each iteration of the outer loop. Show the iteration-versus-accuracy (outer iteration and training accuracy) curve in the same plot as that for batch gradient descent. The training and test data/labels are provided in digits training data.csv, digits training labels.csv, digits test data.csv and digits test labels.csv.
(g) What can you conclude about the convergence rate of stochastic gradient descent versus batch gradient descent? Which one converges faster?
(h) Show the Lagrangian function for minimization problem (1) and derive the dual problem. Your result should have only dual variables in the objective function as well as the constraints. How can you kernelize the soft-margin SVM based on this dual problem?
(i) Apply the soft-margin SVM (with RBF kernel) to handwritten digit classification. The training and test data/labels are provided in digits training data.csv, digits training labels.csv, digits test data.csv and digits test labels.csv. Report the training and test accuracy, and show 5 of the misclassified test images (if fewer than 5, show all; label them with your predictions). You can use the scikit-learn (or equivalent) implementation of the kernelized SVM in this question. You are free to select the parameters (for RBF kernel and regularization), and please report your parameters.
(j) Implement linear discriminant analysis (LDA) using the same data in (i). Report the training and test accuracy, and show 5 of the misclassified test images (if fewer than 5, show all; label them with your predictions). Is there any significant difference between LDA and SVM (with RBF kernel)? Using implementation from libraries is NOT allowed in this question. You can use pseudoinverse during computation.
2024-02-21