Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

CSE 5523: Machine Learning - Homework #1

Due: 11:59pm 02/13/2024

Homework Policy: Please submit your solutions in a single PDF file named HW_1_name.number.pdf (e.g., HW_1_zhang.12807.pdf) to Carmen. You may write your solutions on paper and scan it, or directly type your solutions and save them as a PDF file. Submission in any other format will not be graded. Working in groups is fine, but each member must submit their own writeup. Please write the members of your group on your solutions. For coding problems, please append your code to your submission and report your results (values, plots, etc.) in your written solution. You will lose points if you only include them in your code submissions.

1) Nearest neighbor & distance metrics [10 points].   Given four labeled training data instances, ([5, 2]⊤, “square”), ([4, 0.5]⊤, “cross”), ([6, 4]⊤, “circle”), ([4, 5]⊤, “diamond”), where each of them is a point in the 2D space (i.e., R2) and labeled by a “shape”, please determine the label (i.e., “shape”) of the test data instance [3, 2]⊤ based on the nearest neighbor rule. See Figure 1 for illustration.

(a) [2 points] What is the label if L1 distance is used?

(b) [2 points] What is the label if L2 distance is used?

(c) [2 points] What is the label if L∞ distance is used? L∞ norm of one vector is defined as the largest magnitude among each element of a vector.

(d) [2 points] What is the label if cosine distance is used? Given two vectors x and x ′ , their cosine distance is defined as 1 − .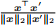

(e) [2 points] What is the label if the following Mahalanobis distance is used? Given two vectors x and x ′ , their Mahalanobis distance is defined as (x − x ′) ⊤A(x − x ′). Here, please consider A as .

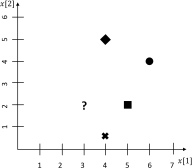
Figure 1: A training set with four labeled data instances and a test data instance (i.e., the question mark).

2) Maximum Likelihood Estimation [10 points].   Consider a random variable X (possibly a vector) whose distribution may be written as f(x; θ), where θ is called the parameter. Maximum likelihood estimation is one of the most important parameter estimation techniques. Let X1, ..., Xn be iid (independent and identically distributed) random variables distributed according to f(x; θ). By independence, the joint distribution of the observations is the product

                            (1)

Viewed as a function of θ, this quantity is called the likelihood of θ. It is often more convenient to work with the log-likelihood,

         (2)

A maximum likelihood estimate (MLE) of θ is any parameter

                (3)

where “arg max” denotes the set of all values achieving the maximum. If there is a unique maximizer, it is called the maximum likelihood estimate. Let X1, ..., Xn be iid Poisson random variables with intensity parameter λ. Determine the maximum likelihood estimator of λ.

3) Linear regression with input dependent noise [20 points].

From the probabilistic perspective of linear regression, we have a model in which the output is linearly dependent on the input with respect to the parameters.

y = w⊤x + ϵ                   (4)

We will see in the class if the noise is from a normal distribution (i.e., ϵ ∼ N (0, σ2)), maximizing likelihood estimation leads to the sum of squares loss (or residual sum of square loss) formulation.

Here, we will consider a simple case where y and x are scalars (i.e., x, y ∈ R) but the noise is dependent on the input such that ϵ ∼ N (0, σ2x 2 ). That is, the standard deviation scales linearly with the input. We observe N independent training examples denoted as Dtr = {(xi , yi)} Ni=1. The model is

y = wx + ϵ.

Let’s assume x is IID sampled from a known distribution with a probability density p(x).

(a) [5 points] Write an expression for the likelihood of data p(Dtr; w) in terms of p(x), σ, xi , yi , w, N, and π.

(b) [5 points] Find the maximum likelihood estimate wML of weights w.

(c) [5 points] Assuming that the prior distribution of w is N (0, α2), express the posterior distribution of w, i.e., p(w|Dtr) in terms of p(x), σ, α, xi , yi , w, N, and π.

(d) [5 points] Find the MAP estimate wMAP of weights w.

4) Weighted Linear Regression [10 points].   Consider a linear regression problem in which we want to weigh different training examples differently. Specifically, suppose we want to minimize

                     (5)

In class, we worked out what happens for the case where all the weights (ri ’s) are one. In this problem, we will generalize some of those ideas to the weighted setting. In other words, we will allow the weights ri to be different for each of the training examples.

Suppose we have a training set {(xi , yi);i = 1, · · · , N} of N independent examples, but in which the yi ’s were observed with different variances. Specifically, suppose that

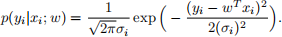                   (6)

In other words, yi has mean w T xi and variance (σi) 2 (where the σi ’s are fixed, known constants). Show that finding the maximum likelihood estimate of w reduces to solving a weighted linear regression problem. State clearly what the ri ’s are in terms of the σi ’s.

5) Naive Bayes as linear classifiers [15 points].

Given a training set Dtr = {(xn ∈ RD, yn ∈ {+1, −1})} Nn=1 for binary classification, let us fit a Naive Bayes model to it; i.e., , where p(x[d]|y) is a Gaussian distribution N (µd,y, σ2d). That is, we assume that for each dimensiond, the two one-dimensional Gaussian distributions (one for each class)

(a) [6 points] p(y|x) can be re-written as 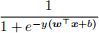 (y ∈ {+1, −1})

(b) [6 points] What are the corresponding w and b?

Your answers should be based on µd,y, σd, and λ. For w ∈ R D, you may simply write the expression of w[d] for a specific d.

6) Naive Bayes Classifier [35 points].

Download the files spambase.train and spambase.test.

The file spambase.train contains 2000 training data and spambase.test has 2601 test data. Both datasets have 58 columns: the first 57 columns are input features, corresponding to different properties of an email, and the last column is an output label indicating spam (1) or non-spam (0). Please fit the Naive Bayes model using the training data.

As a pre-processing step, quantize each variable to one of two values, say 1 and 2, so that values below the median map to 1, and others map to 2. Please aggregate the training and test test to obtain the median value of each variable, and then use the median to quantize both data sets.

(a) Report the test error (misclassification percentage) of Naive Bayes classifier. As a sanity check, what would be the test error if you always predicted the same class, namely, the majority class from the training data?