Mat104 vår 2024 Obligatorisk innlevering 1
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Obligatorisk innlevering 1
Mat104 vår 2024
Innleveringsfrist fredag 2. februar klokka 23.59
Dette er den første av fire obligatoriske innleveringar i MAT104. For å få ta eksamen i MAT104 må alle fire innleveringane vere godkjent. Obligatorisk innlevering 1 kan leverast i grupper på høgst 3 personar. Skriv namn på alle medlemmane i gruppa på innleveringa. Pass på at alle medlemmane i gruppa blir registrert når De leverer i Canvas.
Alle svara skal grunngjevast. Ta med så mykje mellomrekning at framgangsmåten kjem tydeleg fram. Obligatorisk innlevering 1 skal leverast i Canvas som ei pdf-fil.
Oppgåve 1
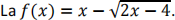
a) Løys likninga f(x) = 2.
b) For kva verdiar av x er f(x) < 2?
c) Finn definisjonsmengda Df til funksjonen.
d) Lag ei skisse av funksjonen for x ∈ [2,6].
e) La definisjonsmengda til f vere Df = [2,6]. Bruk skissa i d) til å estimere verdimengda Vf til f.
f) Har funksjonen f(x) ein invers f −1 på intervallet [2,6]? Grunngi svaret.
Oppgåve 2
Forenkle uttrykka nedanfor.
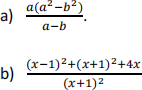
Oppgåve 3
Rekn ut
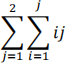
Oppgåve 4
a) Teikn einingssirkelen og marker forteiknet til tan (θ) i kvar av dei fire kvadrantane.
b) Gitt av tan(θ) > 0, finn θ ∈ [0,2π] slik at 2 sin(θ) = tan(θ).
c) Gitt av tan(θ) < 0, finn θ ∈ [0,2π] slik at 2 sin(θ) = tan(θ).
Oppgåve 5
Arkimedes lov seier av ein gjenstand som er heilt eller delvis nedsenka i ei væske får ei oppdrift som er lik tyngda av mengda av den fortrengte væska. Med andre ord, viss ein gjenstand skal flyte må vekta til gjenstanden vere mindre enn vekta til den fortrengte veska.
a) Eit lasteskip veg 5 ⋅ 108 kg. Grunnflata til skipet har ei rektangulær form og er 300 meter langt og breidda er 50 meter (sjå figur). Finn ein funksjon V(h) som gir volumet til skipet som ein funksjon av skipets høgde i meter.

b) Massetettleiken til vatn er 1000 kg/m3 . Kor høgt må skipet vere for å flyte.
c) Anta at skipet er 50 meter høgt. Kor mange konteinarar som kvar veg 105 kg kan ein plasserer i skipet slik at ein har 5 meter klaring til vassflata.
Oppgåve 6
La funksjonen f(t) = 3 + √2(sin(πt) + cos(πt)) vere gitt.
a) Skriv funksjonen f(t) på forma f(t) = C0 + C cos(πt − θ).
b) Finn middelverdien, amplituden, perioden og akrofasen til den harmoniske svinginga.
c) Lag ei skisse av funksjonen for t ∈ [−2,2].
Oppgåve 7
Gitt ulikskapane
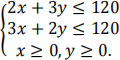
a) Teikn området avgrensa av ulikskapane i xy-planet. Finn koordinatane til kvart hjørne.
b) Finn den største verdien til P(x, y) = 5x + 4y der (x, y) er eit punkt i området frå oppgåve a).
Oppgåve 8
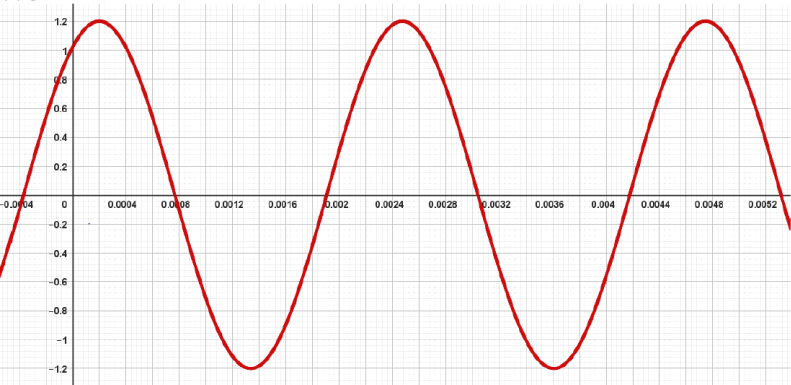
a) Figuren ovanfor viser eit utsnitt av ei lydbølge. Skriv lydbølga på forma til ei harmonisk svinging f(t) = C0 + C cos (T/2π (t − t0)). Bruk figuren for å finne omtrentlege verdiar for C0, C, T og t0.
b) I tabellen nedanfor er frekvensen f = T/1 til nokre tonar oppgitt. Avgjer kva tone som lydbølga ovanfor skildrar.

2024-02-19