MAT237 Multivariable Calculus with Proofs Problem Set 6
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MAT237 Multivariable Calculus with Proofs
Problem Set 6
Due Thursday February 8, 2024 by 23:59 ET
Instructions
This problem set is based on G: Integrals (G7), H: Integral applications (H1 to H3), and I: Integration methods (I1 and I2). Please read the Problem Set FAQ for details on submission policies, collaboration rules, and more.
• Tutorials on Tuesday February 6, 2024 will help you with Problem Set 6. You will work with peers and get help from TAs. Before attending, seriously attempt these problems and prepare initial drafts.
• Submissions are only accepted by Gradescope. Do not send anything by email. Late submissions beyond your grace budget are not accepted under any circumstance. Please read the Problem Set FAQ for details.
• Submit your polished solutions using only this template PDF. You will submit a single PDF with your full written solutions. If your solution is not written using this template PDF (scanned print or digital) then you will receive zero. Do not submit rough work. Organize your work neatly in the space provided.
• Show your work and justify your steps on every question, unless otherwise indicated. Put your final answer in the box provided, if necessary.
Problems
1. (Revised 2024-01-31) Let S ⊆ Rn be a Jordan measurable set. Let f be a bounded real valued function on S.
Show by definition that if f is integrable on S, then f is integrable on So
and 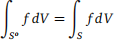 .
.
Use Definition 7.7.1 but do not use Section 7.7 theorems or Lemma 7.5.20. Hint: χSo = χS + (χSo − χS )
2. Let T = {(x, y, z) ∈ R3 : x2 + y2 ≤ 4, x ≥ −1, 0 ≤ z ≤ 9}. The volume of the set T is defined as a 3- dimensional integral, but you can express it as three different 2-dimensional integrals. For each part, formally define correct choices of sets and functions. No justification is required. Do not write down any integrals.
(2a) Express vol(T) = 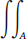 f dA as the volume between z = f (x, y) and z = 0, where A ⊆ R2.
f dA as the volume between z = f (x, y) and z = 0, where A ⊆ R2.
(2b) Express vol(T) = 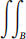 (g2 − g1
)dA as the volume between y = g2
(x, z) and y = g1
(x, z), where B ⊆ R2.
(g2 − g1
)dA as the volume between y = g2
(x, z) and y = g1
(x, z), where B ⊆ R2.
(2c) Express vol(T) = 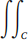 (h2 − h1
)dA as the volume between x = h2
( y, z) and x = h1
( y, z), where C ⊆ R2
.
(h2 − h1
)dA as the volume between x = h2
( y, z) and x = h1
( y, z), where C ⊆ R2
.
3. Let δ : R → [0,∞) be the density of a rectangular object R ⊆ Rn with positive mass. Assume δ is continuous on R aside from a set of zero Jordan measure.
(3a) For a system of point masses at positions x1 , . . . , xN ∈ Rn with masses m1 , . . . , mN , the moment of inertia about the origin 0 ∈ R n is given by

You may take this physical principle for granted. Let P be a partition of R with subrectangles {Ri
}i∈I. Use Riemann sums to exhibit a discrete approximation of the moment of inertia for the object R. When applying ( ), briefly explain what you treat as a point mass and why this assumption is reasonable.
), briefly explain what you treat as a point mass and why this assumption is reasonable.
(3b) Using (3a), derive the integral formula for the moment of inertia I = 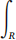 ||x||2δ(x)dV.
||x||2δ(x)dV.
4. Let (Ω,Σ,P ) be a continuous probability space in Rn with probability density function ϕ. Prove that if N ∈ N+ and the sets A1
, . . . ,AN ∈ Σ are pairwise disjoint, then the union 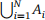 is an event in Σ and
is an event in Σ and
Hint: Proceed by induction on N.
5. Let f : R → R and g : R → R be C1 functions. Assume f ≤ g on the interval [c, d] ⊆ R . Define the set
S = {(x, y) ∈ R2 : c ≤ y ≤ d, f ( y) ≤ x ≤ g( y)}.
(5a) Assume φ : S → R is continuous. Prove that φ is integrable on S.
(5b) Use Fubini’s theorem to show that
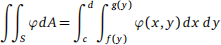
2024-02-08