闪电代写 -代写CS作业_CS代写_Finance代写_Economic代写_Statistics代写_代码代做_IT代写_加急帮助

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MAST90030: Advanced Discrete Mathematics

Assignment 4

Question 1. (50 marks)

For n, t ∈ N, let M be an n × n matrix with entries given by

for i, j ∈ [n].

(a) Describe a set of non-intersecting 3-tuples of binomial paths which are enumerated by det M in the t = 3 case. Sketch all of these 3-tuples. (20 marks)

(b) You are told that det 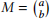for some values a, b ∈ N. Conjecture how a and b depend on n and t. (10 marks)

(c) Describe a bijection from which you then prove the identity (you don’t have to prove that your map is actually a bijection). (20 marks)

Question 2. (50 marks)

For n ∈ N0, define

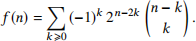
(a) By evaluating f (n) explicitly for a few small values of n, conjecture a simple function of n which equals f (n). (10 marks)

(b) Define a signed set Ω for which ||Ω|| = f (n).

Hint: 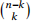is the number of Fibonacci pavings of an n-board using exactly k dimers, and each factor of 2 can be interpreted as arising from colouring certain pavers in two different ways (such as red and blue). (10 marks)

(d) Describe the fixed point set of your sign-reversing involution, and determine its cardinality. Indicate how this proves the identity you conjectured in part (a). (15 marks)