ECO00040M Theory of Finance 2021—22
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
ECO00040M
MSc Degree Examinations 2021—22
Department:
Economics
Title of Exam:
Theory of Finance
Time Allowed:
Twenty-four hours (PLEASE NOTE: Late papers will not be marked)
Time Recommended:
THREE hours
Word limit:
There are no word limits
A complete bibliography is not required for items from the courseís reading list; they can be referred to using author(s) (year) only.
Allocation of Marks:
Please brieáy describe how marks are allocated.
Instructions for Candidates:
Answer FOUR questions, with at least ONE from each section. Each question carries ONE QUAR- TER of the total possible mark.
If you answer more than FOUR questions, only the Örst FOUR answers in the order they appear in the script, will be marked and count towards your Önal mark..
Any answers you do not wish to be included in the marking, must be clearly crossed out.
SECTION A. Answer at least ONE question
1.
(a) [6 marks] The Vasicek model assumes that the short term (spot) interest rate gt is normally distributed. What type of probability distribution do yields obey in this model? When is this assumption likely to be unrealistic? Is it a good model in the current economic environment?
(b) [6 marks] Why would it be more realistic to use the model:
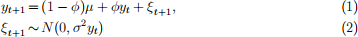
where gt is the short rate and μ > 0?
(c) [6 marks] Assume that the short rate follows the process in Eq. (1) and that the zero- coupon bond prices are exponentially a¢ ne in the short rate, i.e. Dm,t = exp(dm,t ) = exp(-am - bmgt ). Find the expected value of the one-period ahead price Dm-1,t+1 of an m-period discount bond, i.e. Et [Dm-1,t+1].
(d) [7 marks] Assume that the log stochastic discount factor in the economy is given by
where gt is the same shock as in Eq. (1). Recall that the conditional log risk premium adjusted for convexity is given by
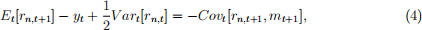
where Tn;t+1 is the log return on then-period zero coupon bond, Tn;t+1 = dn-1;t+1 - dn;t. Find the conditional log risk premium in terms of the model parameters. Is it time- varying?
2. Suppose that we have N risky assets with random returns Ti , means E[Ti] = μi , variances VaT[Ti] = σii , (i = 1, ..., N) and covariances Cov[Ti , Tj ] = σij (i, j = 1, ..., N ; i 
j). Let xi be the share held in the i - th asset. Define the N 根 1 vectors l = [1, ..., 1]0 , x = [x1 , . . . , xN ]0 , r = [T1 , . . . , TN ]0 and μ = [μ1 , ..., μN ]0 , where E[T] = μ. The first (l) is just a summation vector so for example l0x is the sum of the 从-shares or the share of wealth in the risky portfolio. The N x N covariance matrix for the vector of risky returns is represented by Σ = E[(r - μ)(r - μ)0]. Suppose that all investors have the same subjective distribution of returns and have a quadratic utility function:
where yj is a risk aversion coe¢ cient for the j - th investor. The portfolio return Tp is:
Tp = g + xp(')(r - lg),
where g is the risk-free rate on a safe asset.
(a) [6 marks] Prove that if they optimize a linear function of the mean and variance of the percentage return on the portfolio over the same fixed investment horizon using the basic assets of the system, they can do just as well by holding the safe asset and a specially-constructed composite portfolio or mutual fund.
(b) [6 marks] Brieáy outline the implications of result (a) for the fund management industry.
(c) [7 marks] The expected return of j - th investor is
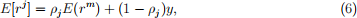
where rm is the return on the mutual fund derived in (a) (the market portfolio) and pj is the proportion of wealth invested in rm. Derive the demand for the risky portfolio pj for the j - th investor in terms of μ, Σ and pj .
(d) [6 marks] If all investors had the same degree of relative risk aversion, yj = y, what would be the demand for the safe asset if it is provided in zero net supply?
SECTION B. Answer at least ONE question
3.
(a) [6 marks] Derive the put-call parity relationship using an arbitrage argument for Euro- pean options and show it on a graph.
(b) [6 marks] Use the put-call parity to establish the lower bound on the European call option. How could you make a proÖt if this bound was violated?
(c) [6 marks] Show that a reverse straddle consisting of a short put and short call with the same strike price K and expiry date T is equivalent to:
. being short one T- maturing forward struck at the forward price F = K and short two of these puts;
. being long one T- maturing forward struck at the forward price F = K and short two of these calls.
(d) [7 marks] You are given the following information on the price of 3 and 6 month European call and put options written on an equity price. The equity is currently trading at 1; 055.
Calls Puts
Strike price: Mar Jun Mar Jun
1; 040 43:6 - 23:2 -
1; 050 37:6 52:2 27:1 31:8
1; 060 33:9 47:7 33:3 -
Your client believes that the volatility implicit in the March option prices is too high. Explain how a strangle could be set up that would allow her to beneÖt if prices stays in the range 1; 040 - 1; 060. Construct and price a butteráy spread for March using put options. Show it on the graph. What is the proÖt from this strategy for di§erent scenarios of the stock price at the expiry date? Is there any arbitrage opportunity here? Discuss.
4. Assume that at time t an oil company share price is St = 500. A major legal judgement concerning an oil spill is due to be announced at time T = 1 year. If this is favourable, its share price will move up to ST;u = 600, otherwise it will move down to ST;d = 300. The risk-free rate is a constant y = 0:10 simply compounded. Consider a riskless portfolio with value Vt at time t and VT at time T that holds θ shares and one put option that costs pt , has a strike price X = 500 such that ST;d < X < ST;u and expires at time T.
(a) [6 marks] Derive the value of θ that makes the portfolio riskless. Find the value of the portfolio at t and T, Vt and VT :
(b) [6 marks] Find the price of the put option at timest and T, pt and pT ;.
(c) [6 marks] Find the prices of contingent claims. Interpret the sum of all contingent claims Check that the contingent claims price all securities, i.e. the stock, the safe asset and the put option;
(d) [7 marks] Find the risk-neutral probabilities held at time t for the two states at time T. Do they sum up to one? Check that the risk-neutral probabilities price all three assets.
2024-02-02