CS 6390, Spring 2024: Homework 1
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
CS 6390, Spring 2024: Homework 1
Assigned: Thursday, January 11, 2024 (25 points total)
Due in Canvas by 11:59pm on Monday, January 29, 2024
(Automatic penalty-free extension until
11:59pm on Wednesday, January 31, 2024)
All homeworks must be done independently. You may post clarifi-cation questions on Piazza, but be sure to make your post instructor-only if it includes part of your solution.
This homework assignment consists of two written exercises. Use the Canvas site to turn in a PDF file containing your written solutions. Scanned images of handwriting are acceptable so long as they are clearly legible.
1 Syntax and Semantics (12 points)
Here is a simple language, whose syntax you have seen before, involving integer addition with let bindings. Take careful note of the semantics, which are given in the form of contextual dynamics; they may differ from what was seen in a lecture example.

(As always, we can insert ad-hoc parentheses in case of AST ambiguity.)
First, a few comprehension questions on ⇒, the steps-to relation:
a) Can (3 + 7) + (4 + 2) step to (3 + 7) + 6? (1 point)
b) Can (3 + 7) + (4 + 2) step to 10 + (4 + 2)? (1 point)
c) Can let x := 3 in ((2 + 2) + x) step to let x := 3 in (4 + x)? (1 point)
d) Is the steps-to relation deterministic, i.e., is it the case that e1 ⇒ e2 and e1 ⇒ e3 implies e2 = e3? Why or why not? (1 point)
NOTE: for e2 = e3 to be true, both e2 and e3 must denote the same program, i.e., the same abstract syntax tree (AST).
Begin to augment the preceding language by adding a special ‘if0’ expression, with syntax of your choice. An if0 expression should be an AST node with 3 children (sub-expressions). Do so by extending the expression syntax:
e) e ::= . . . |
Now add semantics to govern how if0 behaves: an if0 expression yields its second child once the first child has reduced to 0, whereas an if0 expression yields its third child once the first child has reduced to an integer other than 0. You should be able to achieve this behavior by adding 2 local transition rules and 1 new context form (1 point for each).
f) →
g) →
h) K ::= . . . |
Instead of small-step semantics, we could instead define ⇓, the reduces-to relation, via big-step semantics:

Encode the same behavior of if0 as before, but this time using big-step semantics. You can do it with two rules. (1 point)
i) 
Now, demonstrate the behavior of the new language feature by evaluating an example.
j) Write an expression p, with variables x and y free in p, such that p would yield 42 if x and y were bound to integers satisfying y = −2x, and 0 otherwise. (1 point)
k) Define the expression e0 to be let x := −3 in let y := 6 in p. Show the small-step evaluation of e0 as a sequence of expressions e0 ⇒ e1 ⇒ . . . ⇒ 42. (1 point)
l) Show the big-step evaluation of e0 as a proof tree of e ⇓ i terms, with the goal e0 ⇓ 42. (1 point)
2 Typing Rules (13 points)
Here is a definition of a simple arithmetic language with integers, floats, and booleans. Some of its features should be familiar by now; others are new, so take careful note of the definition.
Syntax:
Val v ::= i | f | b (integers, floats, booleans)
Expr e ::= x | v | e1 + e2 | let x := e1 in e2 | if0 e1 then e2 else e3 | round e
Transition rules:

Contextual semantics:

(Partial) type system:

Define a typing rule for the round operator to allow for explicitly casting a float to an integer. (1 point)
a) ———— ty-round
Notice that ty-plus allows us to add two ints to get an int, or to add two floats to get a float. Define two more typing rules so that an up-cast to float automatically happens when int and float expressions are added together. For example, 0.3 + 4 results in a float, even though 4 is an int. (1 point each)
b) ———— ty-upcast1
c) ———— ty-upcast2
Define a typing rule for the if0 construct. Be sure to check the type of all three subexpressions. An if0 expression should type-check only if the test value is an integer and if the two branches are of the same type, either integer, boolean, or float. (1 point)
d) ———— ty-if0
It happens to be the case that for our language, the following typing rule is provably admissible:

If a program is well-typed under some assumptions, it is also well-typed under extra assumptions. What we mean by “admissible” is that though this is not an actual typing rule in our language, it is the case that whenever it is possible to prove the hypothesis, it is also possible to independently prove the conclusion. Therefore, we allow ourselves to use ty-weakening as if it were a typing rule.
e) Construct the proof tree for 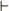 (let x := 5 in let x := true in x) : bool. It will be necessary to appeal to ty-weakening, because of the double-definition of x and the hypothesis on ty-let that x not be in Γ. (3 points)
(let x := 5 in let x := true in x) : bool. It will be necessary to appeal to ty-weakening, because of the double-definition of x and the hypothesis on ty-let that x not be in Γ. (3 points)
But what if we wanted to “overload” x so that both its definitions are kept, and whether we use the int binding or the bool binding depends on how and where we use x? In an attempt to do this, your friend removes the ‘x not in Γ’ hypothesis from ty-let so that it now reads:
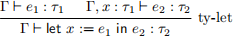
But your friend does not make any changes to the syntax or semantics, which seems unwise.
f) Construct the proof tree for 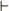 (let x := 5 in let x := true in x) : int, which is only possible because of the change to ty-let. (3 points)
(let x := 5 in let x := true in x) : int, which is only possible because of the change to ty-let. (3 points)
Notice that we now have a program which belongs to two different types!
Theorem: (Preservation) If e ⇒ e' and e : τ and e' : τ' , then τ = τ' . That is, a typed expression keeps its type after taking a step.
g) This theorem held true prior to redefining ty-let. Does preservation still hold? If so, argue why the change to ty-let has no affect on this theorem. If not, illustrate a counterexample to preservation. (3 points)
2024-01-30