Homework 1
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Homework 1
Due: Thursday, Feb 1, 2024 at 12:00pm (Noon)
Written Assignment
Introduction
The purpose of this assignment is to fortify your background in statistics, linear algebra, runtime complexity, socially responsible computing, and programming with NumPy. A strong grasp of these subjects is essential for your success in the course.
You may be able to find answers to these problems by searching for the problem text or consulting a large language model. Please search instead for the concepts being applied; the goal is not to solve these specific problems but to review principles that will be fundamental to the course.
Problem 0: Collaboration Policy
Every student enrolled in CSCI 1420 is expected to know and abide by the course collaboration policy. Your assignments will not be graded if you do not meet this expectation.
Please review the course collaboration policy available at this link and include the following signed statement as your answer to Problem 0:
By signing with my Banner ID below, I agree to abide by the CSCI1420 Collaboration Policy as published on the course website. I also agree to not include my real name on assignments in the course and instead will use my Banner ID on any applicable submissions to preserve anonymity in grading.
Signed: *Your Banner ID Here*
Problem 1: Review of Probability and Statistics
(12 points)
a. Recall Bayes’ Theorem, which asserts that, for events A and B ,

Consider coffee beverages purchased by New Yorkers. Suppose that we have a distribution P on these beverages, where P(coffee is hot) = P(coffee is cold) = 1/2.
the beverages have an equal probability of being hot or iced as well as a 1/7 probability of being a latte (which can be served either hot or iced).
i. Steve bumps into two New Yorkers drinking coffee. What is the probability that both of their coffees are hot?
ii. Kevin bumps into two New Yorkers drinking coffee. One New Yorker’s coffee is hot. What is the probability that both of their coffees are hot?
iii. Thomas bumps into two New Yorkers drinking coffee. At least one of the New Yorkers’ coffees is iced. What is the probability that both of their coffees are iced?
iv. Emma bumps into two New Yorkers drinking coffee. At least one of the New Yorkers’ coffees is a hot latte. What is the probability that both of their coffees are hot?
Hint: None of the four parts have the same answer.
b. Suppose Z1 ,...,Zk are independent standard normal random variables. This means that E[Zi] = 0 and Var(Zi ) = 1. Let
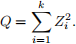
Derive an expression for E[Q] in terms of k.
Hint: Apply the linearity of expectation. Recall that Var(Z1 ) = E IZ1(2)]− (E[Z1])2 = 1 .
Remark: Q as defined above follows the Chi-Squared Distribution .
Problem 2: Review of Linear Algebra
(12 points)
a. Consider a matrix A ∈ Rn ×n. Let rank(A) < n. Prove that A has an eigenvalue equal to 0. You may not use the Invertible Matrix Theorem when solving this problem.
Hint: Recall that the rank of a matrix is equal to the number of linearly independent columns of the matrix.
b. Let B ∈ Rn ×n be a symmetric matrix satisfying xT Bx > 0 for all x ∈ Rn such that x ≠ 0. Remember that the eigenvalues of a symmetric matrix are real. Prove that all of the eigenvalues of B are strictly greater than 0. Do not use any theorems for positive definite matrices.
c. Let C ∈ Rn ×n be a symmetric matrix. Assume that C has n unique eigenvalues. Prove that all of the eigenvectors of C are orthogonal.
Hint: Begin your proof by considering the equations
Cv1 = λ 1 v1
Cv2 = λ2 v2
where (λ1 , v1) and (λ2 , v2) are two different eigenpairs of C. Then, multiply the second equation by 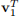 .
.
Problem 3: Runtime Complexity
(14 points)
The Fibonacci sequence can be defined by the recurrence relation F(n) = F(n − 1) + F(n − 2) for n ≥ 2, with F(0) = 0 and F(1) = 1. We can make use of the fact (likely first noted by Edsger Dijkstra) that
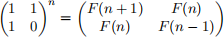
for any positive integer n. So, to compute F(n), we can compute 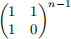 and return the upper left number in the matrix.
and return the upper left number in the matrix.
Describe an algorithm to compute F(n) for arbitrary n that uses fewer than O(n) additions and multiplica- tions (don’t worry about the size of the integers), and prove that it satisfies this complexity bound. That is, prove a sublinear complexity bound in terms of n on the number of additions and multiplications this algorithm performs. Feel free to search for such an algorithm, but please generate the proof of the complexity bound yourself.
Problem 4: Socially Responsible Computing
(7 points)
While planning the construction of the Fukushima nuclear power plant, data scientists were interested in determining the highest earthquake magnitude the plant should be able to withstand.
To achieve this, they used continuous regression models using data of earthquake magnitudes recorded over the years. The graphs below plot two models, where the y-axis represents annual frequency and the x-axis represents earthquake magnitude. The magnitude ranges 4.5 up to the rare 9.5. The diamonds denote the observed frequencies of earthquakes of different magnitudes, and the solid line represents the predictions of the frequencies by each model.
Source: Silver, N. (2012) . The Signal and the Noise: Why So Many Predictions Fail–but Some Don’t. New York, NY: Penguin Press.
Scientists referred to one of the two graphs above to inform the plant’s engineering and determined that the plant should withstand an earthquake of up to 8.6. In March 2011, the Fukushima nuclear power plant was hit with a 9.1 earthquake—one the most severe nuclear accidents since Chernobyl.
a. The scientists’ determination for the plant’s design to withstand an earthquake of 8.6 magnitude led to a detrimental consequence. Looking at the two graphs, what does each model predict about the probability of an earthquake of magnitude 8.6?
b. Which graph did the scientists use in making their decision for the plant’s design? What went wrong in the modeling, and why should they have referred to the other graph instead?
Hint: Think of things that often go wrong with choosing and fitting a model to some given data, and make note of the difference in the two graphs.
Programming Assignment
Introduction
The purpose of this portion is to get familiar with NumPy, which we will use heavily throughout the semester.
NumPy is a powerful numerical computing library for Python that provides very efficient, heavily optimized functionalities for large, multi-dimensional arrays and matrices (see np.ndarray), as well as many standard manipulations and linear algebra algorithms (see np.linalg).
It is strongly preferred over “pure Python” implementations (eg. with for-loops) for several reasons. In particular, NumPy leverages several highly optimized low-level libraries (see BLAS and LAPACK) written in languages like C and Fortran to minimize all overhead involved in the operations and computations, since Python is an interpeted language whereas C and Fortran are compiled. Additionally, NumPy arrays will always be much more memory-efficient than Python list’s.
Set up
Python 3.9 and NumPy are necessary for the completion of programming assignments for this course. Python and NumPy can be installed on your own machine via the directions found at this link. For your convenience, we also have a course-wide virtual environment set up on the department machines at /course/cs1420/cs142_env. The environment can be activated from your own folder by running the fol- lowing command: source /course/cs1420/cs142_env/bin/activate.
Stencil Code
You can find the stencil code for this assignment on GitHub classroom at this link. For more details, please see the download/submission guide.
We have provided the following stencil code:
. warmup.py contains 8 functions for you to implement: part_a through part_g. You will implement these functions in the Warm Up: Introduction to NumPy portion of this programming assignment.
. eigenvalues.py contains two functions for you to implement: qr and compute_eigenvalues. You will implement these functions in the Computing Eigenvalues via QR Decomposition portion of this programming assignment.
You should only need to modify code marked with #TODO in warmup.py and eigenvalues.py to complete this assignment. If you make any other edits to the provided stencil code, please make sure to revert them or leave them commented out in the final handin for autograder compatibility.
To test your implementations in eigenvalues.py, you can run python tests.py in a terminal. Make sure you activate the virtual environment first when working over ssh or on a department machine:
source /course/cs1420/cs142 env/bin/activate
Warm Up: Introduction to NumPy
If you have never used NumPy before, please read through the “Getting started” portion of the NumPy user guide before attempting this exercise. For each of the following parts, please implement its associated function in warmup.py.
NumPy is often abbreviated as “np” (i.e., import numpy as np). You may find the following functions par- ticularly helpful: np.arange, np.zeros, np.ones, np.eye, np.sum, np.hstack, np.vstack, np.transpose, np.matmul, np.inner, np.where, and np.dot.
You may not use np.array() (eg. to create the desired Numpy ndarray’s from Python list’s).
a. Create a 1-dimensional matrix containing the values 2 through 6 inclusive. Return the new matrix in function part_a.
b. Create a 4 × 4 matrix where all entries are 1. Return the new matrix in function part_b. c. Create a 6 × 6 identity matrix. Return the new matrix in function part_c.
d. Given matrix A, compute the sum of the values of its columns. Return the answer in function part_d. e. Given matrices A and B, compute C, where C = ATB. Return the matrix C in function part_e.
f. Using either np.vstack or np.hstack, create a 4 × 2 matrix where all the values in the first column are zeros and all the values in the second column are ones. Return the new matrix in function part_f.
g. Given a matrix of floats A, create a new matrix of the same shape where all values greater than 3 .0 are set to 1 and all other values are set to 0. Return the new matrix in function part_g.
Computing Eigenvalues via QR Decomposition
Your task is to finish implementing both the Householder QR decomposition algorithm (lines 2 through 9 in Algorithm 1) and the QR eigenvalue computation algorithm (Algorithm 2). In the stencil, these are contained respectively in qr and compute_eigenvalues in the eigenvalues.py. The lines in Algorithm 1 which you must implement are colored violet. Please note that this problem is intended to serve as a NumPy exercise; therefore, understanding the theory behind the algorithms is not a requirement.
QR Decomposition
Let A e Rn ×n. The QR decomposition of A is a matrix product QR, where Q e Rn ×n is an orthogonal matrix (QT = Q −1) and R e Rn ×n is upper triangular. This factorization is called the QR decomposition.
Below, we present the Householder QR decomposition algorithm. Again, you do not need to understand the mathematics behind this algorithm. The purpose of implementing this algorithm is to gain familiarity with transforming mathematical and algorithmic notation into respective NumPy operations. This includes learn- ing how to multiply matrices, compute norms, and manipulate NumPy arrays using NumPy’s functionalities instead of Python for-loops.
Some notes regarding the notation presented in Algorithm 1:
1. We let yi denote the i-thentry of some vector y, andya:b will denote the subvector y with first element ya and last element yb −1. Note that the vector ya:b should contain b — a entries.
2. Similarly, xi,j will denote the entry in the i-th row and j-th column of some matrix X . Let Xa:b,c:d denote the submatrix of X with upper left corner xa,b and lower right corner xc −1,d−1 . Note that Xa:b,c:d should have dimension (c — a) X (d — b). You can find some examples of this notation on our NumPy guide.
3. Also, Xa:b,j will denote the j-th column of submatrix Xa:b,0:n. Note that Xa:b,j is a vector with b — a entries.
4. Let In ×n denote the n X n identity matrix. Let 0n ×n denote an n X n matrix where all entries are 0. 5. I · I2 denotes the L2 norm. sign(x) evaluates to 1 if x ≥ 0 and 0 otherwise.
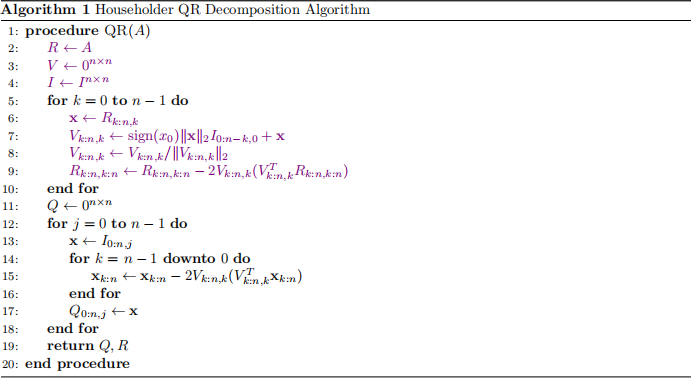
Some notes regarding the implementation of Algorithm 1:
1. The sign( ·) function has been implemented for you in the stencil code. Do not use np.sign.
2. The NumPy equivalent for Xa:b,c:d is X[a:b, c:d] (see Python’s slice notation). Similarly, the NumPy
equivalent for Xa:b,c is X[a:b, c]. If you wish to index the entire j-th column of X, use X[:, j].
3. The vector Vk:n,k in line 9 should be treated strictly as a column vector. Note that calling V[k:n, k] will return a 1-dimensional NumPy array. To transform Vk:n,k into a column vector, you can call V[k:n, k].reshape(-1, 1). Generally, if x satisfies x.shape = (a,), then you can reshape x into an a X 1 NumPy array by calling x.reshape(-1, 1).shape = (a, 1).
4. You should not use V[k:n, k] /= np.linalg.norm(V[k:n, k]). You should instead use V[k:n, k] = V[k:n, k] / np.linalg.norm(V[k:n, k]).
Computing Eigenvalues with QR Decomposition
We can leverage the QR decomposition to approximately compute the eigenvalues for a matrix A e Rn ×n. First, we let Atemp = A. Then, we iteratively update Atemp a total of m times, where the k-th iteration constitutes the following updates:
QR = Atemp ,
Atemp = RQ.
Under certain conditions, Atemp will converge to an upper triangular matrix. Then, the eigenvalues of A are the diagonal elements of Atemp. The complete algorithm is presented below.

Grading Breakdown
The grading breakdown for the assignment is as follows:
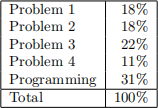
Problem 0 is ungraded but must be submitted for your assignments this semester to be graded.
Handing In
You will turn in your final handin via Gradescope, which you should have been automatically added to through Canvas. If you have questions about using Gradescope or have not been added, please ask on Edstem. For this assignment, you should have written answers for Questions 1, 2, 3, and 4. Please submit the written portion to “Homework 1” on Gradescope.
For the programming, you should submit your code (warmup.py and eigenvalues.py) to “Homework 1 Code” on Gradescope.
Anonymous Grading
You need to be graded anonymously, so please do not write your name anywhere on your handin.
Obligatory Note on Academic Integrity
Plagiarism — don’t do it.
As outlined in the Brown Academic Code, attempting to pass off another’s work as your own can result in failing the assignment, failing this course, or even dismissal or expulsion from Brown. More than that, you will be missing out on the goal of your education, which is the cultivation of your own mind, thoughts, and abilities. Please review this course’s collaboration policy and if you have any questions, please contact a member of the course staff.
2024-01-27