COMS30033-J Machine Learning 2023
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
January 2023 Examination Period
Department of Computer Science
3rd Year Examination for the Degrees of
Bachelor in Computer Science
Master of Engineering in Computer Science
COMS30033-J
Machine Learning
Part 1: Short questions (5 marks each)
Question 1 (5 marks)
George Box famously stated that “All models are wrong, but some models are useful”. Which theorem does this refer to (2 marks)? Briefly explain what are its implications for the development of models in machine learning (3 marks).
Question 2 (5 marks)
In logistic regression what is the model output y(x) equal to (2 marks)? Give the cost (or error) function for logistic regression and explain the different terms (3 marks). Note: Take a deterministic (i.e. non-probabilistic) formalism here.
Question 3 (5 marks)
Figure 1 shows a Bayesian network structure (i.e. directed acyclic graph). Write down all pairs of variables which are independent, conditional on {D, F}.
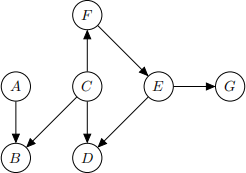
Figure 1: Directed acyclic graph for Question 3
Question 4 (5 marks)
Let S be the sample covariance matrix of some data where S is:

Let u1 = (−0.5365, 0.8439) be the first principal component of the data (approximated to 4 significant figures). What is the variance of the data when projected onto one dimension using this principal component? (Give your answer using 4 significant figures.)
Question 5 (5 marks)
State one important similarity and one important difference between probabilistic PCA and ICA.
Question 6 (5 marks)
Describe the k-means algorithm in at most 60 words. (You may use equations; these will not count towards the word count.)
Question 7 (5 marks)
Here is a dataset with 2 datapoints where each row is a datapoint:
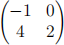
Let ϕ1(x) =  and ϕ2(x) = x1x2. Write down the Gram matrix for this data using the kernel associated with the feature map ϕ where ϕ(x) = (ϕ1(x), ϕ2(x)).
and ϕ2(x) = x1x2. Write down the Gram matrix for this data using the kernel associated with the feature map ϕ where ϕ(x) = (ϕ1(x), ϕ2(x)).
Question 8 (5 marks)
Below is a diagram of an incomplete CART decision tree classifier. We want to grow the tree to a maximum depth of 2 (2 decision nodes deep) using the CART algorithm. The classifier is supposed to decide automatically whether an email is ‘important’ to the user or not. Below the tree diagram is also a table showing the data points in the training set.
(a) Draw the rest of the tree that we learn using CART (4 marks).
(b) What is the residual error of the tree on the training set after adding this node (1 mark)?
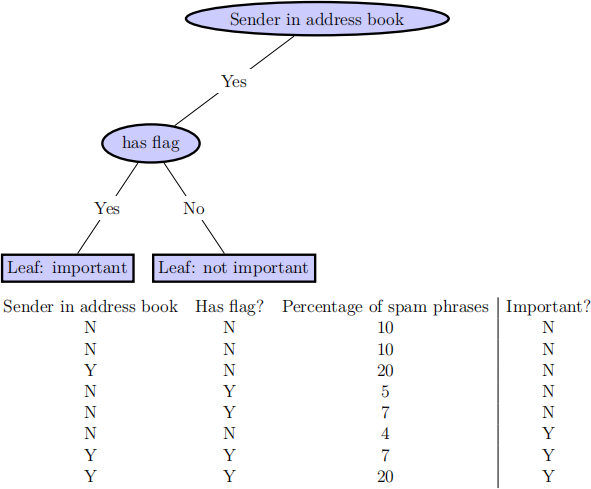
Question 9 (5 marks)
Suppose we have trained a mixture of experts for a binary classification task. There are three experts (base classifiers) in the mixture. We want to classify a new data point i with a feature vector xi = [2.012, 334, 7177, 0.02, 0.01]. The experts’ predictions are:
p(yi = +ve|xi , expert1) = 0.2
p(yi = +ve|xi , expert2) = 0.5
p(yi = +ve|xi , expert3) = 0.3
The mixture weights for each expert for data point i are:
p(expert1|xi) = 0.6
p(expert2|xi) = 0.3
p(expert3|xi) = 0.1
(a) Compute the posterior probability of the positive class, p(y = +ve), that the mix-ture of experts will output. Show your working. (3 marks)
(b) Why do we assign different mixture weights, p(experti |x), to each expert in the mixture of experts? Briefly state the function of the mixture weight terms. (2 marks)
Question 10 (5 marks)
We are using a hidden Markov model (HMM) to label words in a piece of text as either "placename" or "other". We tag the following sequence of words: "that" "is" "new" "york" "for" "you". The HMM labels "york" as "placename" but labels "new" as "other". This is incorrect, as both words are part of a single placename, "New York".
You investigate the error, and find that the HMM’s estimated transition matrix is:
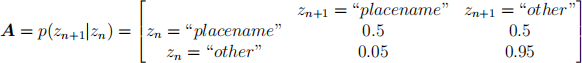
Rows in A correspond to values of the state at the current time-step, n, and columns to values of the state at the next time-step, n + 1.
You also find that the emission probabilities for “new" and “york" are:
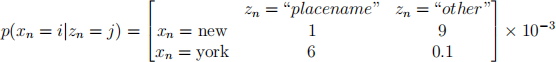
Explain why you think “new" is incorrectly labelled, and why the model correctly labels “york”. Refer to the transition matrix, A, and the emission distribution, p(xn = i|zn = j).
Part 2: Long questions (10 marks each)
Question 11 (10 marks)
You are given a very simple neural network (Figure 2) with only one input x and one output neuron y with a linear activation function σ. Consider that the network is currently receiving the following data point x = 0.1 and that its target should be t = 1. Assume a standard mean squared error, E = 2/1 (y − t) 2 .
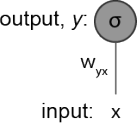
Figure 2: Schematic of a simple artificial neural network.
(a) To perform gradient descent on the weights in your network you must compute wyx = wyx −  . What is the numeric value for
. What is the numeric value for  ? Assume that the current wyx = −0.9 and that there is no bias. Your answer only needs to be approximate (e.g. 0.06 instead of 0.062348). Make sure to explain the equations and steps used to arrive at your solution. (5 marks)
? Assume that the current wyx = −0.9 and that there is no bias. Your answer only needs to be approximate (e.g. 0.06 instead of 0.062348). Make sure to explain the equations and steps used to arrive at your solution. (5 marks)
(b) How do you test for generalisation (i.e. performance on unseen datasets)? (1 mark)
What strategies can you use to help ensure that your ANN generalises well? And why does it work? (2 marks) (3 marks)
(c) Are artificial neural networks parametric or non-parametric models?
Explain why. (2 marks)
Question 12 (10 marks)
(a) Draw the Gaussian mixture model as a Bayesian network using plate notation. Do not forget to include nodes which represent the model parameters. It is fine to use a single node to represent a random variable which has matrix or vector values. State which nodes of your Bayesian network are observed and which not. You do not need to represent the number of Gaussians in the mixture model. You do not need to define priors over model parameters. (5 marks)
(b) The PyMC documentation tells us that the sample method (which performs MCMC) “generates a set of parallel chains”. What does this mean (2 marks) and why does PyMC do it (3 marks). (5 marks)
Question 13 (10 marks)
(a) Let c > 0 be some constant and let k1 be a kernel function. Define the function k as follows: k(x, x ′ ) = ck1(x, x ′ ). Prove that k is a kernel function. (5 marks)
(b) Explain what a support vector is. (2 marks)
(c) When soft margins are allowed an optimisation problem equivalent to the following is solved when learning with an SVM:
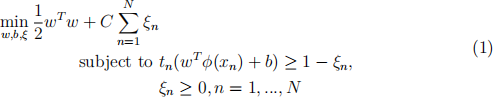
Explain what each of w, C, ξn, xn, tn, ϕ, b represent. (3 marks)
Question 14 (10 marks)
Figure 3 shows values recorded from a noisy sensor over a sequence of time-steps from 1 to T. The sensor readings xt are each marked with an ‘x’. We have fitted a linear dynamical system (LDS) to this data using a Kalman filter. Its predictions of the latent variable, zt , given observations up to time t, are shown as solid points with a line.
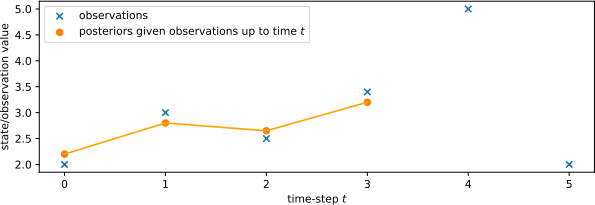
Figure 3: Kalman filter partially applied to a sequence of noisy sensor observations.
(a) Roughly draw the plot from Figure 3, and add the LDS prior prediction of latent state z4 before observing sensor reading x4. Mark the point with a ’p’. (2 marks)
(b) Add the LDS posterior prediction of z4 given the observation x4, by extending the line graph and marking the prediction with a solid point. Your point does not need to be precise, just a rough estimate relative to the other points in the plot. (2 marks)
(c) Add the LDS posterior prediction after Kalman smoothing given observations x4 and x5. Mark the point with a ‘+’. Again, your point does not need to be precise. (2 marks)
(d) What assumption do both hidden Markov models (HMMs) and linear dynamical systems (LDS) rely on? (2 marks)
(e) What is the key difference between an HMM and an LDS? (2 marks)
Question 15 (10 marks)
Imagine we are building a new training dataset and have crowdsourced two different labels for each data point from different annotators. We now want to infer the ’ground truth’ label, ti , for data point i using the Dawid and Skene model.
There are two classes, 0 and 1. The annotators have provided the labels c (1)i = 1, and c (2)i = 0, where c (k)i means the label provided by annotator k for data point i.
According to our trained model, M, the likelihood of the annotator’s labels is:
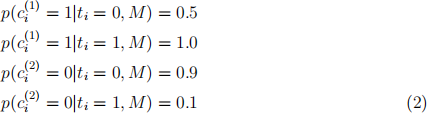
The prior probability of each class according to the model M is:
p(ti = 0|M) = 0.6
p(ti = 1|M) = 0.4
(a) Compute p(ti = 1|c (1)i = 1, c (2)i = 0, M), the posterior probability that the true label is 1, given the annotators’ labels, and the model defined above. (7 marks)
(b) What do the likelihoods in Equation 2, above, tell us about the accuracy of our two annotators? (3 marks)
2024-01-20