Electronic Structure Theory Sheet 4 2022/23
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Electronic Structure Theory
Sheet 4
2022/23
Due: Friday Week 5, 12pm
1 Aims
In this exercise, building on the lectures in weeks 4 and 5, you will investigate the pseudopotential concept, plane wave basis sets, and Brillouin zone sampling, as well as analysing simple bulk properties of different materials, all with the QuantumESPRESSO (QE) software package.
We use some of the standard test systems in computational solid state physics, the quartz phase of SiO2, two relevant phases of Sn (the diamond phase, α-tin, and the tetragonal phase, β-tin), and silicon.
2 Instructions
2.1 Preparations
Copy the QE input file archive into an appropriate sub-directory and unpack it.
user@login:~> mkdir exercise -4
user@login:~> cd exercise -4
user@login:~>/home/dc154/dc154/shared/temp_dc137 _shared/ inputs_ Exercise4.zip .
user@login:~> unzip inputs_ Exercise4.zip .
In the subdirectories quartz, sn and si, have a look at the input files quartz.scf-mt. in, quartz.scf-us. in, alpha-sn.scf. in, beta-sn.scf. in, and si.scf. in, as well as the
job submission scripts, QE-scf. slurm.
For quartz,it is provided two different sets of pseudopotentials (PP’s): norm-conserving PP’s of the Martins-Troullier (MT) type, Si. pbe-mt gipaw. UPF![]() and O. pbe-mt. UPF, and ultrasoft PP’s of the Vanderbilt (VAN) type, Si. pbe-van gipaw. UPF
and O. pbe-mt. UPF, and ultrasoft PP’s of the Vanderbilt (VAN) type, Si. pbe-van gipaw. UPF![]() and O. pbe-van gipaw. UPF
and O. pbe-van gipaw. UPF![]() .
.
Both treat the Si3s23p2 and O2s22p4 electrons as valence space, and keep the other elec- trons as part of a frozen core. For tin, it is provided one ultrasoft PP of the Vanderbilt type, Sn. pw91-n-van.UPF, with 14 valence electrons (4d105s25p2 ).
These PP’s were created by others, using the PBE and PW91 exchange-correlation (XC) functionals, respectively. A large library of QE PP’s, of various types and made with a variety of XC functionals, can be found online: http://www.quantum-espresso. org/pseudopotentials/
3 Tasks
3.1 Quartz and Tin: Convergence Tests
Study the total energy’s dependence on the basis set size, i.e. the plane wave cutoff energy, and the sampling of reciprocal space through a regular Brillouin zone k-grid. To that end, modify the input files to run QE calculations with variable plane wave energy cutoffs (given by the keyword ecutwfc in the input files) and k-grids (specified as a triplet n1 n2 n3 0 0 0 in the K POINTS section of the input file). Note that QE’s total![]() energies are given in Rydbergs/unit cell.
energies are given in Rydbergs/unit cell.
1. For quartz,you should investigate a cutoff range of approximately Ec = 20 ... 200 Ry. Assume that the total energy of the highest plane wave cutoff represents a ”con-verged” value. Relative to this value, how large does the plane wave cutoff need to be, using either PP, to achieve convergence of the total energy to within 10 meV, and to within 1 meV, per SiO2 formula unit? Do the ultrasoft PP’s require a smaller basis set, and how long do the calculations take using the respective nec-essary energy cutoffs?
2. For tin, you have input files for both the α- and the β-phase. The former has the diamond structure and the latter has, well, the β-tin structure. For both, you should investigate a cutoff range up to about 200 Ry. Relative to the ”converged” value (i.e. achieved with the largest cutoff) how large does the plane wave cutoff need to be for either phase to achieve convergence to within 5 meV/atom? Now look at the energy difference between the two phases – how large does the cutoff energy need to be to converge the energy difference between α- and β-tinto within 1 meV per atom, relative to its ”converged” value? Which phase is more stable, and is this in agreement with the known phase diagram of tin? Remember these are ground-state calculations, T = 0 K if you will, and should reproduce the low-temperature behaviour of materials.
3. Next, study the dependence of the total energy on the Brillouin zone sampling, while keeping a constant plane wave cutoff as determined in the previous steps. Use only the ultrasoft PP’s for SiO2. Modify the input files to run QE calculations with different k-point grids. For all compounds, choose isotropic meshes of the form (N,N, N), using approximately N = 1 ... 16. The number of k-points used are listed in the output file; how many are used in each calculation? Why is this number significantly smaller than N3 ? What k-point grid sizes are needed to converge the total energy to within 1 meV per atom? How does the convergence behaviour of the total energy with respect to k-point grid size compare to changes in the plane wave cutoff?
3.2 Silicon: E(V) Equation of State
We want to obtain the equation of state E(V) of silicon and, by fitting it to known models, extract information about the equilibrium lattice constant and bulk modulus. To this end, perform a series of total energy calculations at various unit cell volumes for the Si-diamond structure by editing the input file si.scf. in in the si subdirec- tory accordingly, spanning a range of about ±30% around the experimental volume – or approximately ±10% around the experimental lattice constant, which is given as celldm(1) in your input file (unit: Bohrs).
Once you have finished these calculations, plot the total energy data points against volume and fit them with the three equations-of-state discussed in the week 5 lectures. All of those express energy as function of relative linear compression η = (V/V0 )1/3 .
. The Murnaghan EOS:
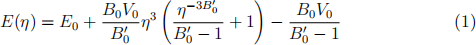
. The third-order Birch-Murnaghan EOS:
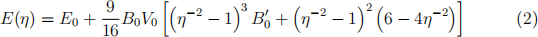
. The Vinet EOS:
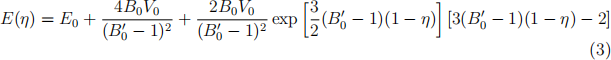
Compare the results for equilibrium volume V0, energy E0 , bulk modulus B0 , and its pressure derivative B0(′) across the different EOS expressions. How do your results for V0 and B0 compare to the experimental values, V0 = 20.0 A(˚)3 /atom and B0 = 100 GPa?
3.3 Silicon: Bulk Properties
Estimate the longitudinal sound velocity in silicon from the relation

where ρ is the mass density of the solid at the calculated equilibrium conditions. How does this compare to experiment?
Use cL as obtained above to estimate silicon’s Debye temperature ΘD from the relation

where we have used the Debye wave vector kD , which in turn is defined via

and n = N/V0 is the atomic number density of silicon at equilibrium. How does ΘD from your calculations compare to the experimental value?
4 Submission
Submit a summary of your results through LEARN, addressing the questions posed in the previous section. Submit a single document (preferrably PDF) including tabulated data, figures, and discussion, as appropriate.
5 Marking Scheme
. Quartz-SCF: required plane wave cutoff energies; comparison MT vs US pseudopo- tentials; calculation times; discussion. [6]
. Sn-SCF: required plane wave cutoff energies for both phases; energy difference convergence; stability; discussion. [6]
. K-point sampling for quartz and Sn: k-point grid convergence; discussion. [10]
. Si-EOS: E(V) data and fits, comparison to experiment. [12]
. Si observables: results, comparison to experiment. [6]
Total marks: 40, count for 20% of the course grade.
2024-01-19