Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

Introduction to Ring Theory (MATH 228): Assignment 5

There are seven questions; answer them all. The assignment is due at 23:59 MT on Tuesday 12th October.

1. Suppose that a non-empty set R together with binary operations + (addi-tion) and · (multiplication) satisfies all the axioms of a ring except possibly axiom A2, commutativity of addition. In this case, we strengthen axiom A3 to say that a + 0 = 0 + a = a for all a ∈ R, and also strengthen axiom A4 to say that, for all a ∈ R, there is b ∈ R such that a + b = b + a = 0. Assume also that R has a multiplicative identity, i.e., an element 1 such that 1 · a = a · 1 = a for all a ∈ R.

(a) Use the two distributivity axioms in one order to show that

(1 + 1) · (x + y) = x + x + y + y.

for all x, y ∈ R. (Do not assume commutativity of addition.)

(b) Now use the distributivity axioms in the opposite order to show that

(1 + 1) · (x + y) = x + y + x + y

for all x, y ∈ R. (Do not assume commutativity of addition.)

(c) Deduce from parts (a) and (b) that addition is commutative in R. Hint: Use the strengthened axioms A3 and A4 described above.

2.      (a) Let X be a set.

(i) Show that 2A = 0 for all A ∈ P(X).

(ii) Deduce that (A+B)² = A²+B² for all A, B ∈ P(X). (Remember that P(X) is a commutative ring.)

(b) Let Y be a set with at least two elements. Show that there are non-zero elements A and B of P(Y ) such that A · B = 0.

3. Let R be a ring with just two elements, 0 and 1. Here, 0 is the zero element of the ring, and 1 satisfies 1² = 1. Show that if n is a positive integer, then the equation xⁿ + 1 = 0 has a solution in R. Hint: Which element of the ring is 1 + 1, and how do you know?

4. Let R be a unital ring. Show that the ring S = S(R) has elements e1, e2, e3 satisfying

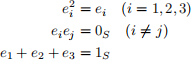
Hint: Think about the standard basis vectors e1, e2, e3 in R³ , which sum to the vector (1, 1, 1). Can you use this idea to find three sequences in S that sum to the identity sequence?

5. Find a solution to the equation a² + b² = 1R in each of the following unital rings R. That is, exhibit an explicit element a ∈ R and an explicit element b ∈ R satisfying the equation. If you are given any restrictions on a and b, adhere to those restrictions.

(a) R = Z. Choose a and b to be non-positive.

(b) R = Q. Choose a and b so that neither is an integer. Hint: If the two shorter sides of a right-angled triangle have lengths 3 and 4, how long is the hypotenuse?

(c) R = F. Choose the functions a and b such that both are continuous and neither is constant. Hint: Think of a well-known identity from trigonometry.

(d) R = P(X), where X = {1, 2, 3}. Choose a and b so that neither is zero.

(e) R = M2(Z), the ring of 2×2 matrices with integer entries. Choose the two matrices so that both are diagonal and neither matrix is zero.

(f) R = M2(Z) again. This time, choose the two matrices so that at least one of them is not diagonal. Hint: Can you think of a non-zero matrix B ∈ M2(Z) such that B² = 0?

6. Characterize the units in S(Z). That is, if α = (an)n ∈ S(Z), what is the condition on the terms an for α to be a unit in S(Z). Explain your answer.

7.      (a) For each x ∈ (Z/7Z)^×, find the least positive integer n such that xⁿ = [1]. You do not need to show your working in this question.

(b) Extra part (no answer required): What do you notice about these integers n in relation to the number of units in Z/7Z?